An asymptote is a line (or curve) that the graph of a relation at some point gets closer and closer to.
An asymptote is a line (or curve) such that as a point moves along the curve (never stopping), the distance from the point to the asymptote approaches zero.
Note that the curve may, or may not, intersect the asymptote, but beyond a certain point will approach the asymptote, never reaching it.
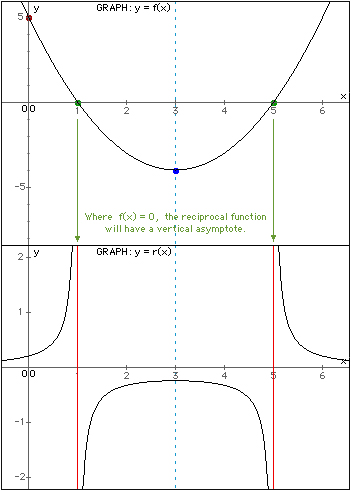
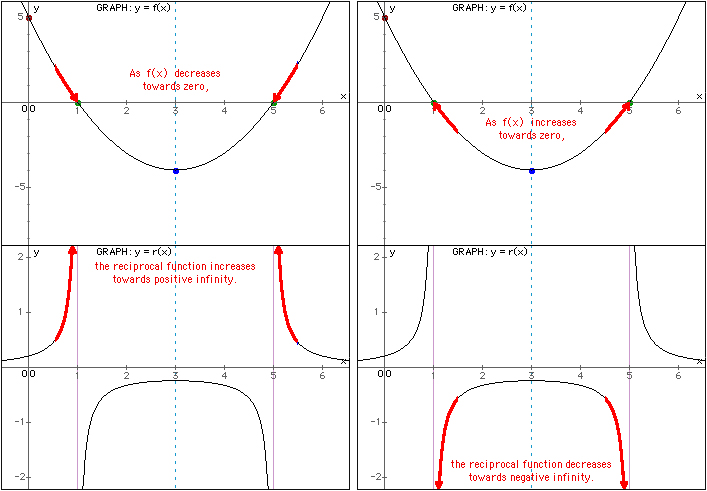
Given a function and the corresponding reciprocal function, the graph of the reciprocal function will have vertical asymptotes where the function has zeros (the x-intercept(s) of the graph of the function).
f(x) = ( x - 3 )2 - 4. r(x) is the reciprocal function of f(x).
f(x) has zeros of 1 and 5 [x-intercepts of ( 1, 0 ), ( 5, 0 )].
r(x) has two vertical asymptotes with equations x = 1 and x = 5.
The graph of a function may have zero, one or many vertical asymptotes.
The graph of a function may have exactly zero or one horizontal asymptote.
The graph of a function will never have more than one horizontal asymptote.
Observe from the graph that as x gets larger and larger (approaching positive infinity) that:
Observe from the graph that as x gets smaller and smaller (approaching negative infinity) that:
Example One: A horizontal line other than the x-axis
Example Two: A slant asymptote
Example Three: A non-linear asymptote
