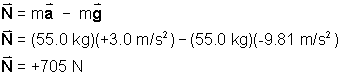Lesson 1 - Elevator
Elevator simulates the motion of an elevator and applies free body analysis
and Newton's second law to determine the relationship between apparent weight,
normal force, and actual weight.
Prerequisites
Students should have a working knowledge of free body diagrams, graphical analysis,
and Newton's second law.
Learning Outcomes
Students will be able to calculate the weight, normal force, and apparent weight
of a person in an elevator during each phase of an elevator trip between floors.
Students will understand why a person's apparent weight changes as the elevator
accelerates. Students will also be able to graphically describe all phases of
motion in a typical elevator trip between multiple floors.
Instructions
Students should understand the applet functions that are described in Help and ShowMe.
The applet should be open. The step-by-step instructions on this page are to
be done in the applet. You may need to toggle back and forth between instructions
and applet if your screen space is limited.
Contents
- Defining Weight, Normal Force, and Apparent Weight
- Making and Using Free Body Diagrams
- Graphical Analysis of the Motion
- Problem Solving
1. Defining Weight, Normal Force, and Apparent Weight
Before starting, make sure that you understand
the precise meanings of the terms that will be used in the lesson.
Weight is the gravitational force exerted
by the Earth on an object. Note that weight is based on Newton's second law ( ). ). |
| Expressed as an equation:
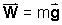
| Quantity |
Symbol |
SI Unit |
| weight |
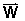 |
N |
| mass |
m |
kg |
| acceleration due to gravity |
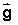 |
m/s2 |
* The acceleration due to gravity at the Earth's surface is -9.81
m/s2. |
| Normal Force is
the force exerted by a surface on another body. For example, when you stand
on the floor, the floor exerts an upward force on you. The normal force is
always perpendicular to the surface. |
| Apparent Weight is the name given to the force
that you exert on another body - perhaps a weigh scale. For example, if
you stand on a bathroom scale, you exert a downward force on the scale
(your apparent weight) which is equal in magnitude to the normal force
that the scale exerts on you. Therefore, the magnitude of the apparent
weight equals the magnitude of the normal force. |

Using the definitions above, complete the following calculations and explanations.
-
Calculate the weight of a 60.0 kg person at the surface of the Earth.
-
Calculate your weight at the surface of the Earth.
- Suppose you jumped onto your bathroom scale. Would the scale initially
indicate a high weight and then settle down to your actual weight? (Note:
the initial weight would be your apparent weight at the moment you landed
on the scale.)
- Your apparent weight can be greater than your actual weight.
True or False.
Explain.

On the applet, adjust the passenger "mass" slider ( )
and observe how the weight and normal force vectors respond. What
happens to the normal force as the weight of the passenger changes? )
and observe how the weight and normal force vectors respond. What
happens to the normal force as the weight of the passenger changes?

Use the applet to simulate a variety of up and down elevator trips at
different accelerations for a 60.0 kg passenger. Carefully observe
the magnitude of both the normal force and passenger weight throughout
each trip.
- Is the passenger's weight constant throughout a
typical elevator trip regardless of any acceleration?
- Is the normal force constant throughout a
typical elevator trip?
- Essentially, an elevator causes motion by
adjusting only the normal force. True or False.
Explain.
|
2. Making and Using Free Body Diagrams
The applet will now be used to investigate the forces
that act throughout a typical elevator trip. Set up the following
parameters on the elevator applet,
- Double click the mass slider and enter the mass of the occupant as 60.0 kg.
- Double click the acceleration slider and set the acceleration at 4.0 m/s2.
- Click "Up" (
 )
to start the elevator. )
to start the elevator.
The elevator will accelerate, coast, and then come to a stop. This represents
a typical elevator trip. Observe carefully what happens to the Weight
(W) and Normal force (N)
vectors that are drawn on the applet during each phase of the trip. Once
the elevator has stopped, you may wish to reset the elevator and observe
the motion again. |

Use the terms greater than, equal to, or less than
to compare the size of the normal force when the elevator is at rest to
the size of the normal force as the elevator:
- accelerates upward
- coasts
- slows down
|

The apparent weight of the passenger equals the magnitude of the normal
force acting on the passenger. Use the terms greater than,
equal to or less than to compare the passenger's weight
when the elevator is at rest to the apparent weight when the elevator:
- accelerates upward
- coasts
- slows down
|

Based on your observations from exercise 5 and actual experience riding
in an elevator, which force (weight or apparent weight)
do you feel when the elevator:
- accelerates upward
- coasts
- slows down
|

Complete the table by drawing the free-body diagrams in each phase of
the elevator trip. Indicate the relative magnitude (size) of the
normal force and the weight on each diagram.

accelerating upward (+)
(speeding up) |

coasting /
resting
(constant speed) |

accelerating
downward (-) (slowing down) |
The net force acting on the occupant is the sum of all force acting on
the occupant. This is described by:
 (1)
(1)
Rewrite equation (1) using Newton's second law where,
" " is
substituted for " " is
substituted for " " "
" " is substituted
for " " is substituted
for "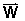 " "
(______) = (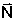 )
+ (______) (2) )
+ (______) (2)
Manipulate equation (2) in terms of the Normal force (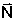
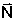 = (______) - (______) (3)
= (______) - (______) (3)
Equation (3) can be used to determine the apparent weight of a passenger
when the acceleration ( ) of the elevator
is known. For example, what is the apparent weight of a 55.0 kg person
on an elevator that is accelerating upward at 3.00 m/s2? ) of the elevator
is known. For example, what is the apparent weight of a 55.0 kg person
on an elevator that is accelerating upward at 3.00 m/s2?
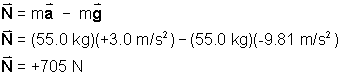
|

Calculate the Normal force using equation (3) and the values for (m) and
( ) in the applet for each phase of the elevator
trip. The value of ) in the applet for each phase of the elevator
trip. The value of 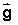 is -9.81
m/s2 . The mass of the passenger should be set at 60.0
kg and the acceleration ( is -9.81
m/s2 . The mass of the passenger should be set at 60.0
kg and the acceleration ( ) of the elevator
should be set at 4.0 m/s2. Note that the direction and
magnitude of the acceleration will be different in each phase of the trip
and that they are indicated in the table below. ) of the elevator
should be set at 4.0 m/s2. Note that the direction and
magnitude of the acceleration will be different in each phase of the trip
and that they are indicated in the table below.
accelerating upward
(+)
(speeding
up)
( = + 4.0 m/s2) = + 4.0 m/s2)
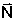 = =
|
coasting / resting
(constant
speed)
( = 0.0 m/s2) = 0.0 m/s2)
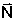 = =
|
accelerating
downward (-)
(slowing down)
( = - 4.0 m/s2) = - 4.0 m/s2)
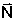 = =
|

Verify your answers from exercise 8 by recording the Normal force value
from the scale reading that is shown in the upper left corner of the applet.
Click "Pause" ( )
to "freeze" the motion in each phase of the trip if you have
trouble reading the scale. )
to "freeze" the motion in each phase of the trip if you have
trouble reading the scale.
accelerating upward (+)
(scale reading)
N = |
coasting / resting
(scale reading)
N = |
accelerating downward (-)
(scale reading)
N = |
|

Two of the scale readings from exercise 9 indicate apparent weight while
the third is actual weight.
- Which two scale readings are apparent weights?
- Which scale reading represents the "heavy" sensation you would feel
on this elevator trip?
- Which scale reading represents the "light" sensation you would feel
on this elevator trip?
3. Graphical Analysis of the Motion
| Graphical analysis of velocity, acceleration, and scale
readings clearly illustrate three phases of motion involved in a typical
elevator trip between multiple floors. For example, to the right are
three graphs taken from data collected for a 50.0 kg passenger
traveling up several floors in an elevator that can accelerate at
5.00 m/s2.
The first phase of motion is an upward (+) acceleration as the
elevator departs from the starting floor. The second phase of motion
is uniform motion as the elevator travels between floors at a constant
speed. Finally, the third phase of motion is a downward acceleration
as the elevator approaches the destination floor.

On all three graphs, label phase 1, phase 2, and phase 3.
velocity vs. time
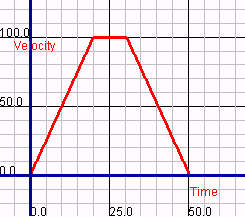
acceleration vs. time
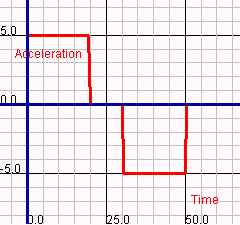
normal force (scale reading) vs. time
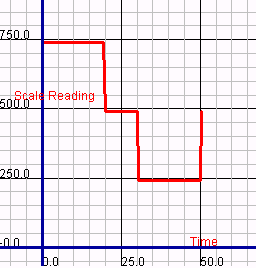
Each phase of motion can be described by an interpretation of all
three graphs. For example,
During phase 1, the passenger experiences an increase in
positive velocity caused by a net positive acceleration that is
caused by a normal force greater in magnitude than the passenger's
weight.
During phase 2, the passenger experiences a constant velocity
with a net acceleration of zero that is caused by a normal force
that is equal in magnitude to the passenger's weight.

Using the same terminology, describe phase 3.
During phase 3, . . .
|

Complete the following three graphs for an 80.0 kg passenger
traveling up several floors in an elevator that can accelerate
at 4.0 m/s2.
- Run the simulation in the applet.
- Click "Graph" (
 ). ).
- Select the appropriate axis from the drop-down menus.
- Click "Fit Graph" (
 )
to display the graph. )
to display the graph.
- Label each phase of the motion on each graph.
velocity vs. time
acceleration vs. time
normal force (scale reading) vs. time
|
|
4. Problem Solving
Use the applet for assistance in answering for the following questions.

Calculate the apparent weight of an 80.0 kg person riding in an elevator that
is accelerating upward at a rate of 5.00 m/s2.
(Verify your answer using the applet.)

Use a free body diagram to explain what happens to the apparent weight of
a person if the elevator begins to "free-fall" (accelerating
downward at 9.81 m/s2). (Verify your answer
using the applet.)

Imagine that you are in an elevator that is accelerating upward
at 6.00 m/s2. If your apparent weight is 800 N , what is your
mass? (Verify your answer using the applet.)

A passenger on an elevator experiences an apparent weight of 500 N while accelerating
downward. If the mass of the passenger is 70.0 kg, at what rate
is he accelerating? (Verify your answer using the applet.)

While traveling down between floors at a constant speed, a passenger has a
weight of 800 N . During the acceleration to stop the elevator, the passenger
experiences an apparent weight of 1000 N . Calculate the acceleration of
the elevator. (Verify your answer using the applet.)
Physics 20-30 v1.0
©2004 Alberta Learning (www.learnalberta.ca)
Last Updated: June 16, 2004
 ).
).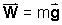


 )
and observe how the weight and normal force vectors respond. What
happens to the normal force as the weight of the passenger changes?
)
and observe how the weight and normal force vectors respond. What
happens to the normal force as the weight of the passenger changes?





 (1)
(1)  " is
substituted for "
" is
substituted for " "
"
 " is substituted
for "
" is substituted
for "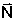 )
+ (______) (2)
)
+ (______) (2) ) of the elevator
is known. For example, what is the apparent weight of a 55.0 kg person
on an elevator that is accelerating upward at 3.00 m/s2?
) of the elevator
is known. For example, what is the apparent weight of a 55.0 kg person
on an elevator that is accelerating upward at 3.00 m/s2?