Students need to have a basic knowledge of angles and be able to use the Pythagorean theorem with basic trigonometry.
Students will be able to define vector quantities. Students will be able to describe vector directions using the Polar (positive), Polar (positive and negative) and the Navigational method. Students will also be able to calculate vector magnitude and direction based on Cartesian components and vice versa.
Students should understand the applet functions that are described in Help and ShowMe. The applet should be open. The step-by-step instructions on this page are to be done in the applet. You may need to toggle back and forth between instructions and applet if your screen space is limited.
Vector quantities include displacement, velocity, and acceleration. They are defined by having both magnitude (size) and direction.
Vector magnitude is expressed in only one way, depending on the quantity. For example, the magnitude of a vector could be expressed in metres ( for displacement), or metres per second (for velocity). However, there are a variety of ways to specify direction. The direction is often specified in terms of an angle, but there are different ways of choosing an angle for a given vector. Consider the three possibilities by completing the following exercise.
|
a. Polar (positive) Directions On the control panel of the applet, select the "Polar (positive)" mode and enter 150 for the magnitude and 240° for the angle. Verify that the display matches Figure 1.
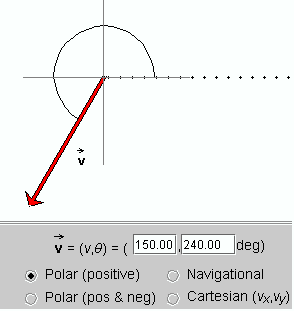
Figure 1 In this mode, an angle is measured from a reference line (shown dotted and pointing east) in the positive, counter-clockwise direction that is indicated by the arc. Angles can range from 0° to 360°. Note: 360° is equivalent to 0°. |
|
b. Polar (positive and negative) Directions On the control panel of the applet, select the "Polar (pos & neg)" mode without changing any of the settings from Exercise 1. Verify that the display matches Figure 2.
Figure 2 In this mode, both positive and negative angles are used. Vectors pointing above the horizontal reference line are assigned positive values between 0° and +180°. Vectors pointing below the horizontal reference line are assigned negative values between 0° and -180°. |
What is the maximum size of an angle that can be specified using the "Polar (pos & neg)" method? To determine this, select the Polar (pos & neg) mode on the control panel and drag the red vector tip through a 360° circle while observing the angle in the control panel.
maximum angle: _______________
Using the applet in the Polar (positive) mode, set a vector that points into the first quadrant. Draw and label the vector magnitude and angle in the table below. Draw the same vector in the Polar (pos & neg) row of the table. Predict and label the angle in the Polar (pos & neg) mode. Repeat this procedure for vectors in the second, third, and fourth quadrants. Verify your answers using the applet.
Polar (positive) specification:
| First Quadrant angle:_________ |
Second Quadrant angle:_________ |
Third Quadrant angle:_________ |
Fourth Quadrant angle:_________ |
Polar (pos & neg) specification:
| First Quadrant angle:_________ |
Second Quadrant angle:_________ |
Third Quadrant angle:_________ |
Fourth Quadrant angle:_________ |
|
c. Navigational Directions On the control panel of the applet, select the "Polar (positive)" mode in the control panel of the applet and enter 150 for the magnitude and 240° for the angle. Then, select the "Navigational" mode, and choose "N of E" (North of East) from among the eight compass directions on the drop-down menu. Verify that the display matches Figure 3. "North of East" means that the angle is measured starting from the East direction and going towards the North direction, but not necessarily stopping there. In the present example, the angle continues past the North direction. Note: the compass labels have been added to Figure 3 for your reference; they will not appear on the applet display.
Figure 3 |
Complete the following table by sketching the vectors and labeling the magnitude and direction. The first one has been completed as an example. Use the applet to verify your answers.
|
a) mag: 75
|
b) mag: 150  |
c) mag: 200 |
d) mag: 75 |
e) mag: 150 |
f) mag: 200 |
Is there more than one way to specify the same navigational direction? Answer this by sketching the following two vectors and labeling the magnitude and direction. Use the applet to verify your answer.
75 @ 30° N of E |
75 @ 60° E of N |
What is another way of indicating 75 @ 25° S of E using an angle less than 90°? Draw and label the vector below. Use the applet to verify your answer.
|
|
Cartesian components are another way to describe a vector quantity. Rather than specifying a vector quantity in terms of magnitude and direction, this method uses scalar components. The applet will be used to describe this method of vector specification.
|
On the control panel of the applet, select the "Polar (positive)" mode in the control panel of the applet and enter 150 for the magnitude and 240° for the angle. Then, select the "Cartesian (vx, vy)" mode on the control panel. Verify that the display matches Figure 4. The projections of the vector onto the x and y axes, shown in green and yellow respectively, are called the scalar components of the vector. They are called scalar components because they are numbers. The scalar components are equal to the x and y coordinates of the tip of the vector if the tail end of the vector is at the origin of the coordinate system, as it is here. The coordinates have been added to the display in Figure 4.
Figure 4 |
The x and y scalar components of a vector 
are denoted vx and vy, respectively. In
the present case, this pair of components has the value:
(vx, vy) = (-75.00, -129.90)
You can use the notation (vx,vy) to denote
the vector , because the vector is fully specified in terms
of its two scalar components. Thus, when required to calculate a vector
you can give the final answer in the form above. There is no need to calculate
the magnitude and direction of the vector because the components contain this
information.
You could state your final answer in the form:
= (-75.00, -129.90)
However, when describing a vector by its two components, it must be understood from the context how the x and y axes are defined. In this case, the axis are defined as number lines with positive and negative directions.
| Given the magnitude and direction of a vector, how are
the components (vx, vy) calculated?
First, make a diagram showing the relevant quantities as shown in Figure 5.
Figure 5 The diagram shows a right-angle triangle containing the vector |
Find this angle using the applet. On the control panel of the applet, select the "Polar (positive)" mode in the control panel of the applet and enter 150 for the magnitude and 240° for the angle. Then select the Navigational mode and (S of W) from the drop-down menu on the control panel.
α = _________
|
Knowing
angle
α
allows you to use basic trigonometry to solve for the vertical component |vy|.
Figure 5 shows that vy is downward and therefore negative: vy = -129.90
|
|
| Basic trigonometry is also used to solve for the horizontal
component |vx|:
Figure 5 shows that vx is directed towards the left and is therefore negative: vx = -75.00
|
|
| The vector components are correctly written as (-75.00, -129.90). | |
Given scalar (vx, vy) components, how
are the magnitude and direction of a vector,
calculated?
| Applying the Pythagorean theorem to the right-angle triangle in Figure
5 gives:
|
| Applying the definition of the tangent to the right-angle
triangle in Figure 5 gives:
OR
|
Given the vector components (-75.00, +200.00), calculate the magnitude and
polar positive direction of the vector. Show your work and use the applet
to verify your answer.
Given the vector components (+65.00, -120.00), calculate the magnitude and
navigational direction of the vector. Show your work and use the applet
to verify your answer.
Given the vector 126.00 @ 65.00° N of E, calculate the vector components.
Show your work and use the applet to verify your answer.
Given the vector 225.00 @ 135.00° W of S, calculate the vector components. Show your work and use the applet to verify your answer.
Physics 20-30 v1.0
©2004 Alberta Learning (www.learnalberta.ca)
Last Updated: June 16, 2004
