The number below is an irrational number.
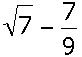
Since it is hard to get a sense of the magnitude of the number (in its exact form), it could be approximated as 1.868.
An approximation to one number is a second number, close enough in value to the first number, that it can be used in its place. The closer the approximation is to the original, the more accurate the approximation.
Approximation is usually used when:
pi (π) is an irrational number (π = 3.141 592 653 589 793 238 462 643 383 279 ...).
One approximation to pi is 3.14. Another approximation to pi is 3.1416.
π - 3.14 = 0.001 592 653 589 793 238 462 643 383 279 ...
3.1416 - π ? 3.14 = 0.000 007 346 410 206 761 537 356 616 721 ...
Since 3.1416 - π < π - 3.14, 3.1416 is a more accurate approximation to π.
The number below is an irrational number.
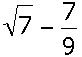
Since it is hard to get a sense of the magnitude of the number (in its exact form), it could be approximated as 1.868.
The number below is a repeating decimal.
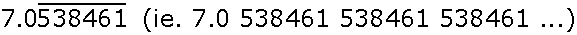
For the purpose of easier calculations, it could be approximated as 1.868.
When measuring the length of the licorice, the licorice "ends" are not consistent and the divisions on the given ruler are not very fine. Only a gross approximation of the length of the licorice is possible. To find the length of the licorice, an approximate number must be used.
An approximate length of the licorice is 14.3 cm.