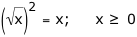The inverse of an operation is one which "nullifies" the outcome of the operation.

Addition and subtraction of the same amount are inverse operations.

Operation: Add five to a number

Inverse operation: Subtract five from a number

If we use the number eleven and perform the operation, a result of sixteen occurs (11 + 5 = 16).

If we perform the inverse operation on the result of the first operation (sixteen), the result of eleven occurs (16 - 5 = 11).

Notice that the number we started and ended with was eleven.

Note also that the number we started with (eleven) was arbitrary.

Replace eleven with "x" and check algebraically:

( x + 5 ) - 5 = x + ( 5 - 5 )

( x + 5 ) - 5 = x

Finally, note that the amount we added and then subracted was arbitrary.

Replace five with "n" and check algebraically:

( x + n ) - n = x + ( n - n )

( x + n ) - n = x

Notice that in this example that the order of the two operations is irrelevant.

Operation: Subtract five from a number

Inverse operation: Add five to a number

If we use the number eleven and perform the operation, a result of six occurs (11 - 5 = 6).

If we perform the inverse operation on the result of the first operation (six), the result of eleven occurs (6 + 5 = 11).

Again notice that the number we started and ended with was eleven.

Also note again that the number we started with (eleven) was arbitrary.

Replace eleven with "x" and check algebraically:

( x - 5 ) + 5 = x - 5 + 5

( x - 5 ) + 5 = x + ( -5 + 5 )

( x - 5 ) + 5 = x

Finally, note that the amount we subracted and then added was arbitrary.

Replace five with "n" and check algebraically:

( x - n ) + n = x - n + n

( x - n ) + n = x + ( -n + n )

( x - n ) + n = x

Multiplication and division by the same amount (other than zero) are inverse operations.

Operation: Multiply a number by two

Inverse operation: Divide a number by two

If we use the number six and perform the operation, a result of twelve occurs (6 x 2 = 12).

If we perform the inverse operation on the result of the first operation (twelve), the result of six occurs (12 ÷ 2 = 6).

Notice that the number we started and ended with was six.

Note also that the number we started with (six) was arbitrary.

Replace six with "x" and check algebraically:

Finally, note that the amount we multiplied and then divided by was arbitrary.

Replace five with "n" and check algebraically:

Notice that in this example that the order of the two operations is irrelevant.

Operation: Divide a number by two

Inverse operation: Multiply a number by two

If we use the number six and perform the operation, a result of three occurs (6 ÷ 2 = 3).

If we perform the inverse operation on the result of the first operation (three), the result of six occurs (3 x 2 = 6).

Again notice that the number we started and ended with was six.

Also note again that the number we started with (six) was arbitrary.

Replace six with "x" and check algebraically:

Finally, note that the amount we multiplied and divided by was arbitrary.

Replace two with "n" and check algebraically:

Squaring a number greater than or equal to zero and finding the square root of a number greater than or equal to zero are inverse operations.

Operation: Squaring a number greater than or equal to zero

Inverse operation: Finding the square root of a number greater than or equal to zero

If we use the number 16 and perform the operation, a result of 256 occurs (16² = 256).

If we perform the inverse operation on the result of the first operation (256), the result of 16 occurs ().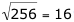

Notice that the number we started and ended with was 16.

Note also that the number we started with (16) was arbitrary.

Replace 16 with "x" and check algebraically:

Notice that in this example that the order of the two operations is irrelevant.

Operation: Finding the square root of a number greater than or equal to zero

Inverse operation: Squaring a number greater than or equal to zero

If we use the number 16 and perform the operation, a result of 4 occurs ().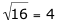

If we perform the inverse operation on the result of the first operation (4), the result of 16 occurs (4² = 16).

Again notice that the number we started and ended with was 16.

Also note again that the number we started with (16) was arbitrary.

Replace 16 with "x" and check algebraically:
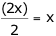
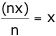
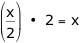
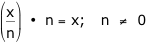
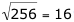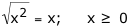
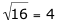