If an operation is represented by the symbol "", then a set (S) is said to be closed with respect to the operation if a b S, for all a, b S

If any two real numbers are added together, the result is a real number.

Examples

6 + -9 = -3

Note that six, negative nine, and negative three are all real numbers.

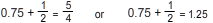
Note that 0.75, one-half, and five-quarters (1.25) are all real numbers.

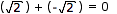
If any two real numbers are multiplied together, the result is a real number.

Examples

6 x -9 = -54

Note that six, negative nine, and negative fifty-four are all real numbers.

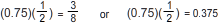
Note that 0.75, one-half, and three-eighths (0.375) are all real numbers.

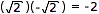
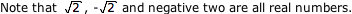
Note that not all number systems are closed under all operations.

Example

The irrational numbers are not closed under addition.

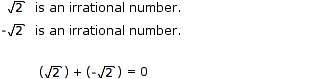
Since 0 is NOT an irrational number (0 is a rational number), the irrational numbers are NOT closed under addition.

Example

The natural numbers are not closed under subtraction.

6 is a natural number.

9 is a natural number.

6 - 9 = -3

Since negative three is NOT a natural number, the natural numbers are NOT closed under subtraction.

Example

The irrational numbers are not closed under multiplication.

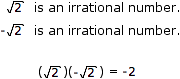
Since negative two is NOT an irrational number (it is a rational number), the irrational numbers are NOT closed under multiplication.