Method One: Graph x2 + 2x - 8 ≤ y [or y ≥ x2 + 2x - 8]
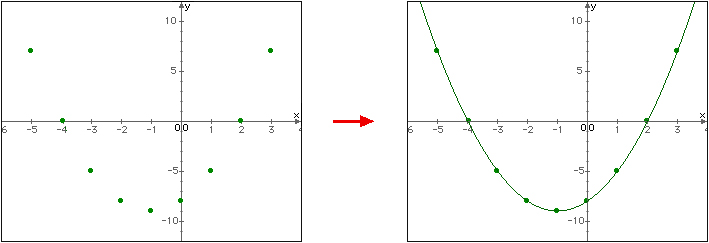
Graph y = x2 + 2x - 8
Find the vertex, x-intercepts and y-intercept, then make a small table of values.
Create a table of values using the x-value of the vertex as a "middle" value.
Plot the locations in the table of values then draw the resulting graph.
Use a solid line as the original inequality isn't strict (y ≥ x2 - 4x + 3)
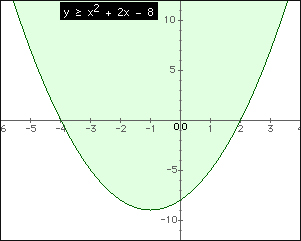
Graph y ≥ x2 + 2x - 8
Choose a "test" location that is not part of the graph of the equality y = x2 - 4x + 3. If the origin is not part of the graph of the equality, it is a "good" location to choose. Substitute the values associated with the test location into the inequality.
y ≥ x2 + 2x - 8 Substitute ( 0, 0 ) into the quadratic inequality
(0) ≥ (0)2 + 2(0) - 8 Simplify
0 ≥-8 (TRUE)
Graph 0 ≥ x2 + 2x - 8 [x2 + 2x - 8 ≤ 0]
View only the x-axis portion of the graph.
Video does not play in this browser or device. Please try another device or upgrade your browser.