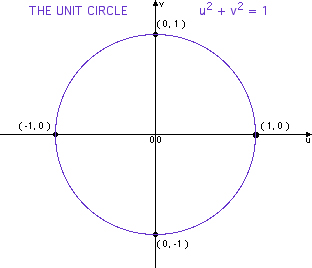
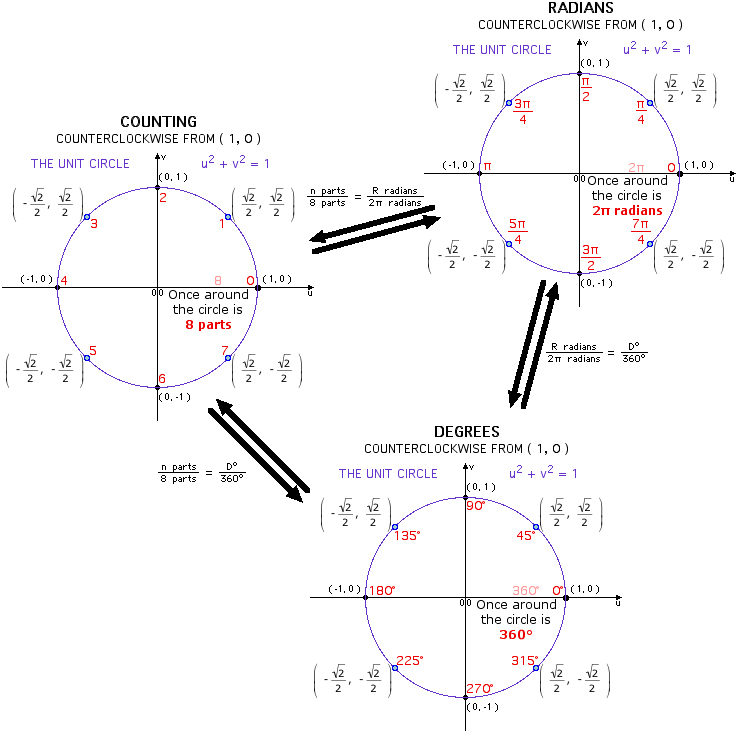
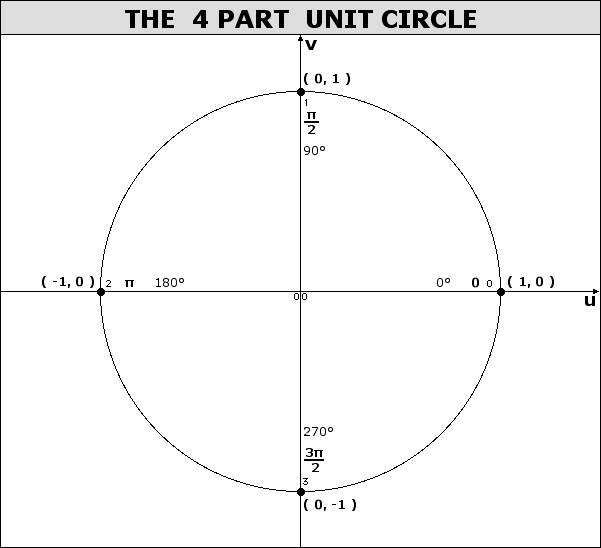
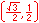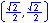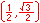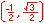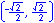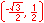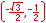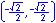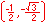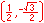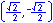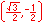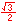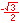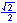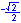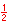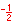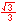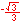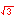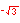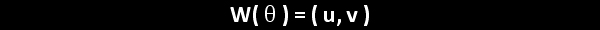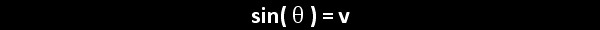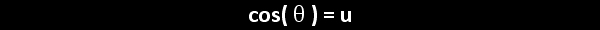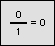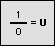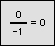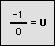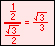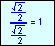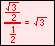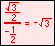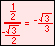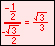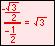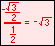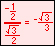In the illustration below, the x and y-axes partition the unit circle into four equal arcs. The locations of intersection are ( 1, 0 ),

( 0, 1 ), (-1, 0 ) and ( 0, -1).

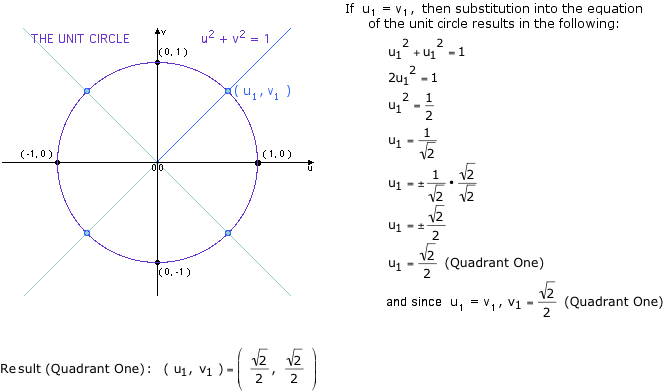
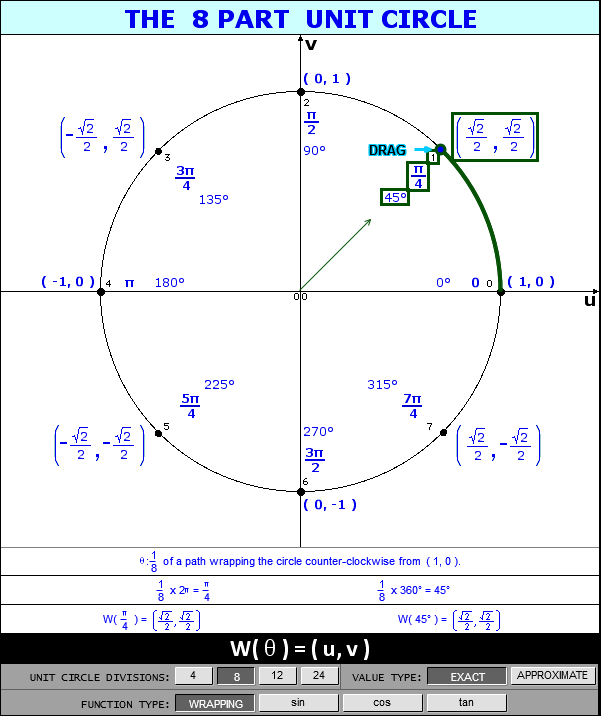
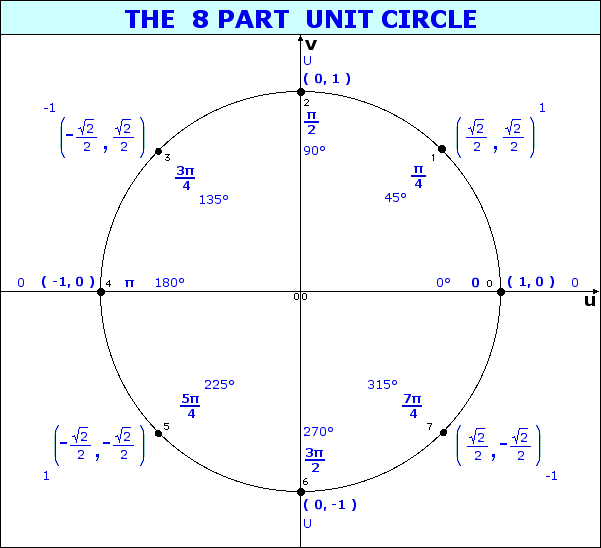
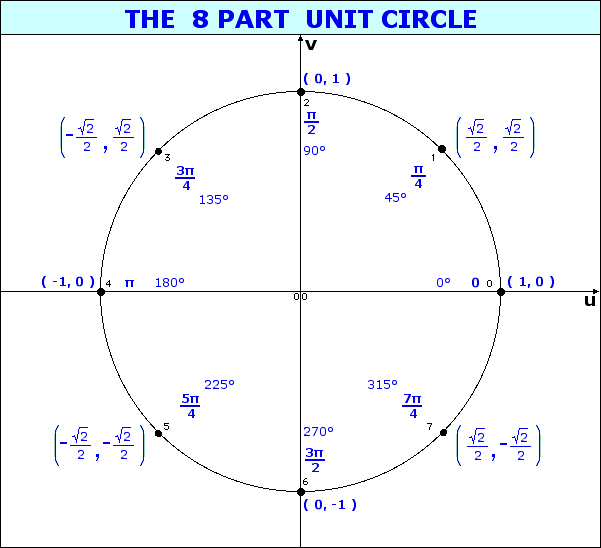
For the eight part circle, each of the the four arcs can be bisected. Observe in the illustration below that the location on the arc in quadrant one that bisects the arc is such that the abscissa will be equal to the ordinate (u₁ = v₁). Note also that in quadrant one, u₁ > 0 and v₁ > 0.

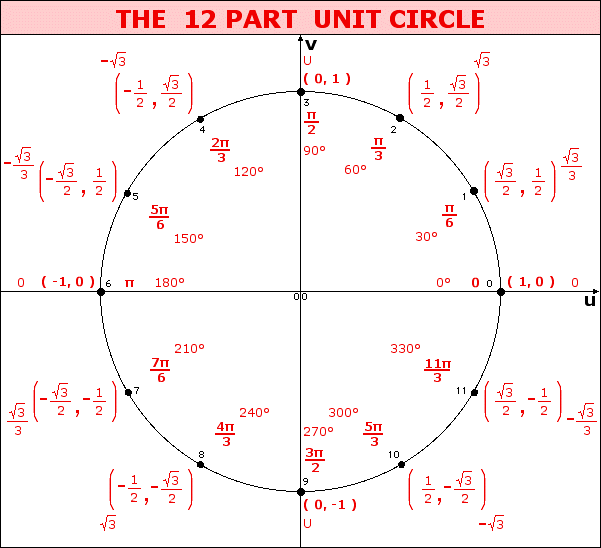
Coordinates of the three remaining locations can be established by symmetry about both the x and y-axes.

Recall that θ can represent either a directed arclength starting from the initial point ( 1, 0 ) or an angle with an initial arm along the positive x-axis. In either case, counterclockwise is positive.

The illustration below illustrates the eight part unit circle:

• counting from zero at ( 1, 0 ), counterclockwise around the circle
• traversing the circle counterclockwise by intervals of π/4 starting from ( 1, 0 )
• traversing the circle counterclockwise by intervals of 45° starting from ( 1, 0 ).