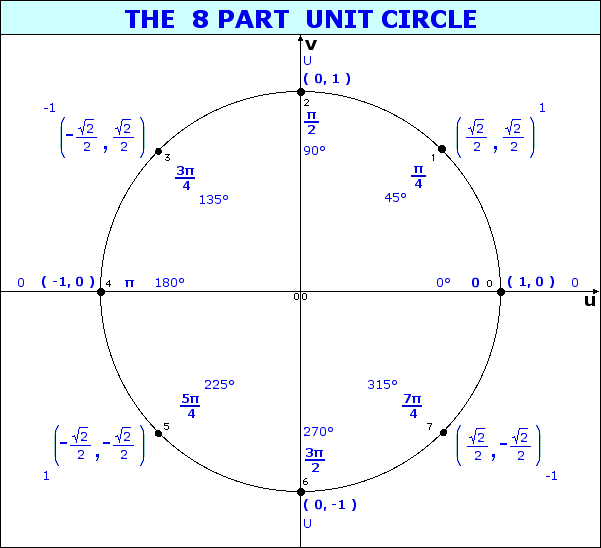
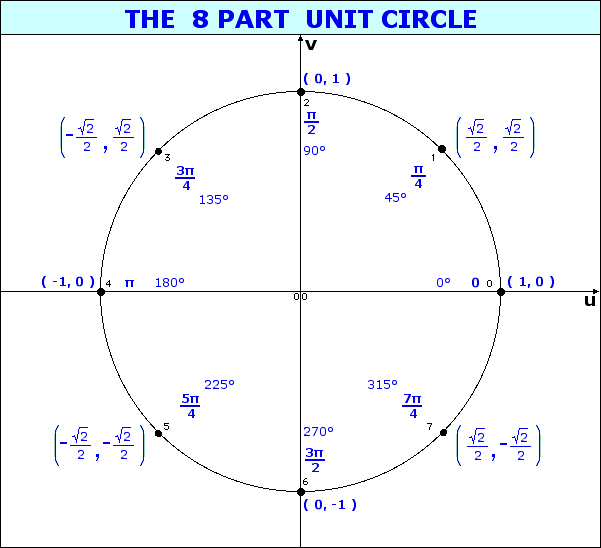
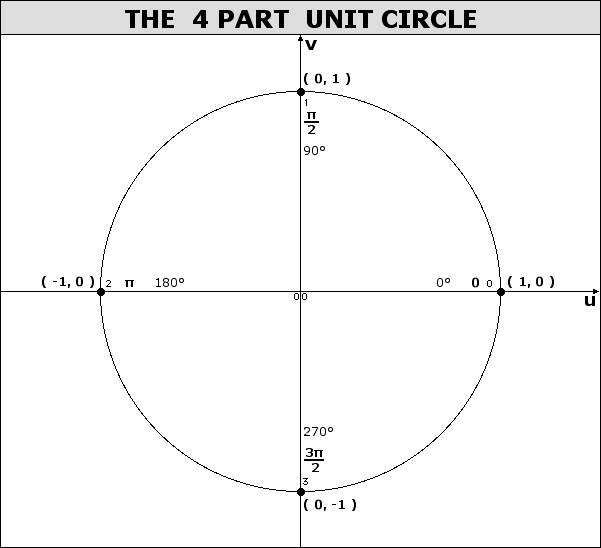
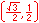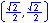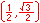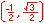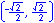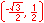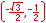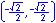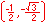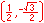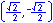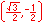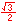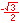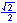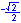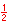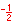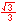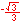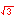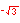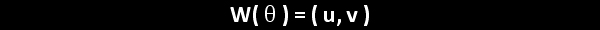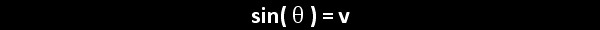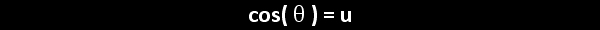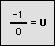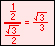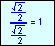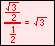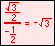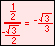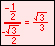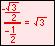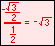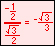In the illustration below, the x and y-axes partition the unit circle into four equal arcs. The locations of intersection are ( 1, 0 ),
( 0, 1 ), (-1, 0 ) and ( 0, -1).
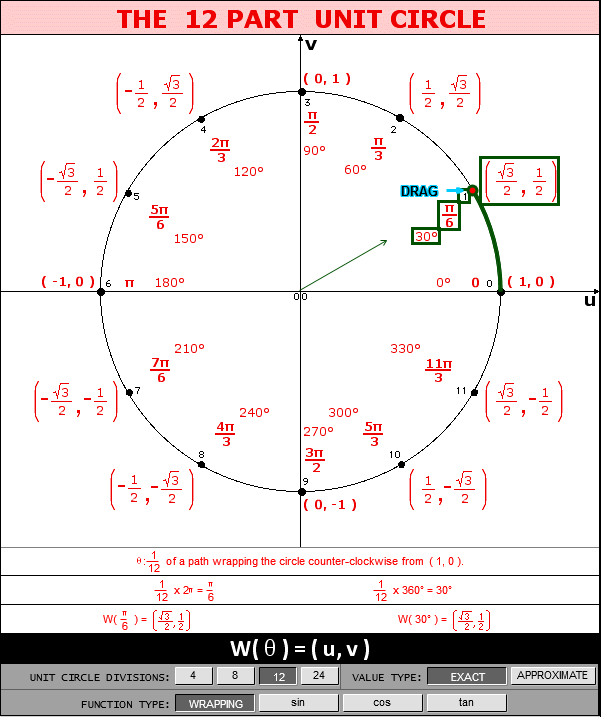
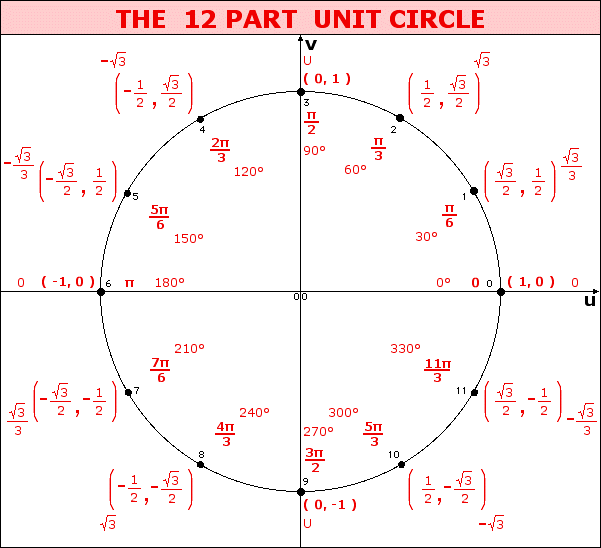
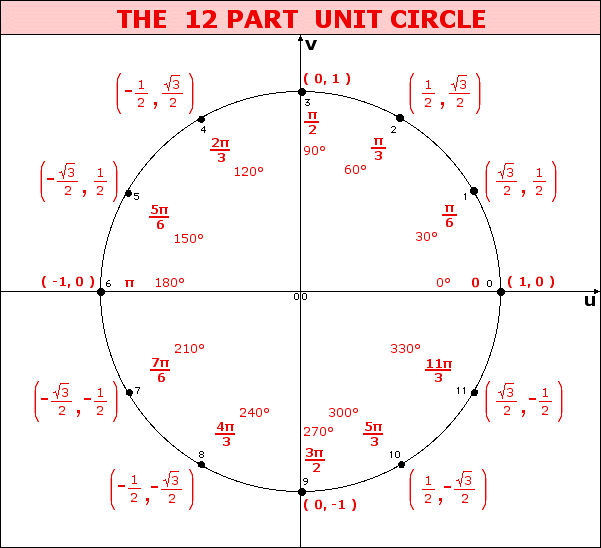
For the twelve part circle, each of the the four arcs can be trisected and the locations determined. Follow the animation below to see how this is done.
Recall that θ can represent either a directed arclength starting from the initial point ( 1, 0 ) or an angle with an initial arm along the positive x-axis. In either case, counterclockwise is positive.
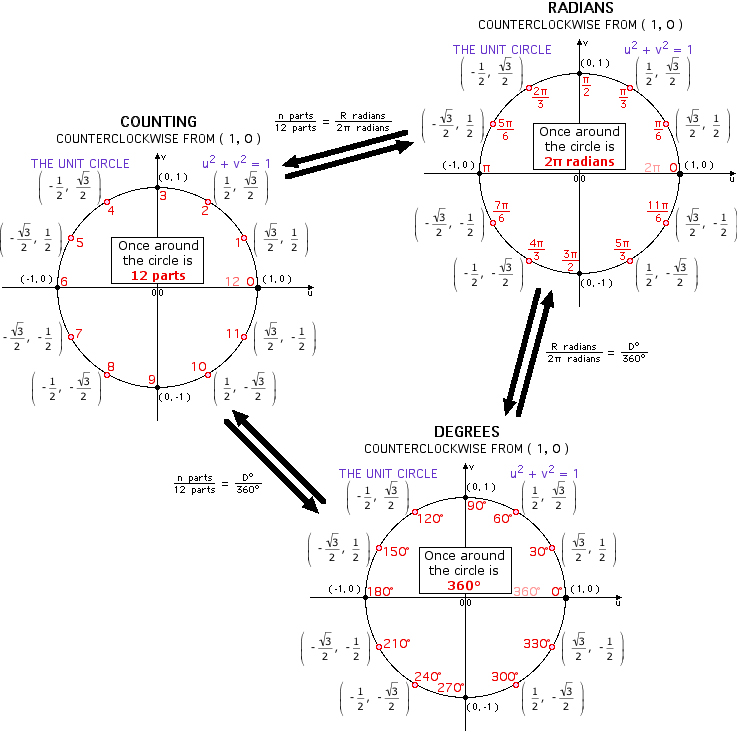
The illustration below illustrates the twelve part unit circle:
- counting from zero at ( 1, 0 ), counterclockwise around the circle
- traversing the circle counterclockwise by intervals of π/6 starting from ( 1, 0 )
- traversing the circle counterclockwise by intervals of 30° starting from ( 1, 0 ).




.gif)
.gif)
.gif)
.gif)