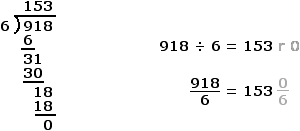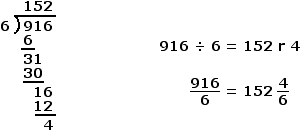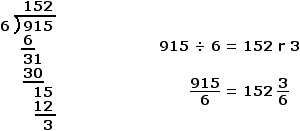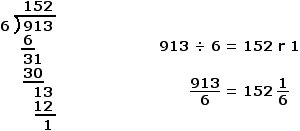A natural number is divisible by 6 if and only if it is divisible by both 2 and by 3.

To determine if a natural number is divisible by 6 requires one to know the "divisibility by 2 rule" and the "divisibility by 3 rule".

The natural number 918 ends in an even number (8). As a result, 918 is divisible by 2 [918 ÷ 2 = 459 r 0].

The sum of the digits of the number 918 is 18 (9 + 1 + 8 = 18). Note that the sum of the digits of the number 18 is 9 (1 + 8 = 9). Since 18 and 9 are divisible by 3, 918 is divisible by 3 [918 ÷ 3 = 306 r 0].

Since 918 is divisible by both 2 AND 3, 918 is divisible by 6.

The natural number 916 ends in an even number (6). As a result, 916 is divisible by 2 [916 ÷ 2 = 458 r 0].

The sum of the digits of the number 916 is 16 (9 + 1 + 6 = 16). Note that the sum of the digits of the number 16 is 7 (1 + 6 = 7). Since neither 16 nor 7 are divisible by 3, 916 is NOT divisible by 3 [916 ÷ 3 = 305 r 1].

Although 916 is divisible by 2, it is NOT divisible by 3. Since 916 is NOT divisible by BOTH 2 and 3, it is NOT divisible by 6.

The natural number 915 ends in an odd number (5). As a result, 915 is NOT divisible by 2 [915 ÷ 2 = 457 r 1].

The sum of the digits of the number 915 is 15 (9 + 1 + 5 = 15). Note that the sum of the digits of the number 15 is 6 (1 + 5 = 6). Since 15 and 6 are divisible by 3, 915 is divisible by 3 [915 ÷ 3 = 305 r 0].

Although 915 is divisible by 3, it is NOT divisible by 2. Since 916 is NOT divisible by BOTH 2 and 3, it is NOT divisible by 6.

The natural number 913 ends in an odd number (5). As a result, 913 is NOT divisible by 2 [913 ÷ 2 = 456 r 1].

The sum of the digits of the number 913 is 13 (9 + 1 + 3 = 13). Note that the sum of the digits of the number 13 is 4 (1 + 3 = 4). Since neither 13 nor 4 are divisible by 3, 913 is NOT divisible by 3 [913 ÷ 3 = 304 r 1].

Since 913 is NOT divisible by either 2 or 3, it is NOT divisible by 6.

716 123 456 789 098 765 432 104 is divisible by 2 since the last digit is even (divisible by 2).

716 123 456 789 098 765 432 104 is divisible by 3 since 108 and 9 are divisible by 3.

NOTE: 7 + 1 + 6 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 4 = 108

NOTE: 1 + 0 + 8 = 9

Since 716 123 456 789 098 765 432 104 is divisible by both 2 AND 3, it is also divisible by 6.

716 123 456 789 098 765 432 107 is NOT divisible by 2 since the last digit is odd (NOT divisible by 2).

716 123 456 789 098 765 432 107 is divisible by 3 since 111 and 3 are divisible by 3.

NOTE: 7 + 1 + 6 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 7 = 111

NOTE: 1 + 1 + 1 = 3

Although 716 123 456 789 098 765 432 107 is divisible by 2, it is NOT divisible by 3. Since it is NOT divisible by BOTH 2 and 3, it is NOT divisible by 6.

The natural number 717 123 456 789 098 765 432 108 ends in an even number (8). As a result, it is divisible by 2.

The sum of the digits of the number 717 123 456 789 098 765 432 108 is 113. Note that the sum of the digits of the number 113 is 5. Since neither 113 nor 5 are divisible by 3, 717 123 456 789 098 765 432 108 is NOT divisible by 3.

NOTE: 7 + 1 + 7 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 8 = 113

NOTE: 1 + 1 + 3 = 5

Although 717 123 456 789 098 765 432 108 is divisible by 2, it is NOT divisible by 3. Since 717 123 456 789 098 765 432 108 is NOT divisible by BOTH 2 and 3, it is NOT divisible by 6.

The natural number 717 123 456 789 098 765 432 105 ends in an odd number (5). As a result it is NOT divisible by 2.

The sum of the digits of the number 717 123 456 789 098 765 432 105 is 110. Note that the sum of the digits of the number 110 is 2. Since neither 110 nor 2 are divisible by 3, 717 123 456 789 098 765 432 105 is NOT divisible by 3.

Since 717 123 456 789 098 765 432 105 is NOT divisible by either 2 or 3, it is NOT divisible by 6.