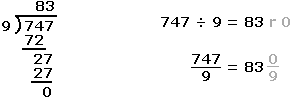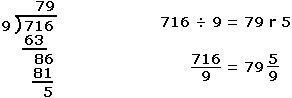A natural number is divisible by 9 if and only if the sum of its digits is divisible by 9.

The sum of the digits of the number 747 is 18 (7 + 4 + 7 = 15). Note that the sum of the digits of the number 18 is 9 (1 + 8 = 9).

747 is divisible by 9 since the sum of the digits of 747 is divisible by 9 (18 ÷ 9 = 2). Note also that the sum of the digits of 18 is divisible by 3 (9 ÷ 3 = 3).

The sum of the digits of the number 716 is 14 (7 + 1 + 6 = 14). Note that the sum of the digits of the number 14 is 5 (1 + 4 = 5).

716 is NOT divisible by 9 since the sum of the digits of 716 is NOT divisible by 9 (14 ÷ 9 = 1 r 5). Note also that the sum of the digits of 14 is NOT divisible by 9 (5 ÷ 9 = 0 r 5).

716 123 456 789 098 765 432 104 is divisible by 9 since 108 and 9 are divisible by 9.

NOTE: 7 + 1 + 6 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 4 = 108

NOTE: 1 + 0 + 8 = 9

717 123 456 789 098 765 432 108 is NOT divisible by 9 since 113 and 5 are NOT divisible by 9.

NOTE: 7 + 1 + 7 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 8 = 113

NOTE: 1 + 1 + 3 = 5