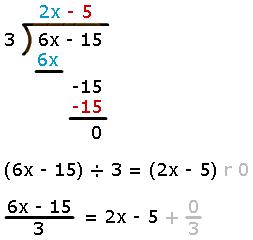
When one term (the "dividend") is divided by another term (the "divisor"), the result is a "quotient" and a "remainder".
When the remainder is zero, both the quotient and divisor are factors of the dividend.
When the remainder is not zero, neither the quotient nor the divisor are factors of the dividend.
6 is the dividend.
3 is the divisor.
2 is the quotient.
0 is the remainder.
Since the remainder is zero, both 2 and 3 are factors of 6.
7 is the dividend.
3 is the divisor.
2 is the quotient.
1 is the remainder.
Since the remainder is not zero, neither 2 nor 3 are factors of 7.
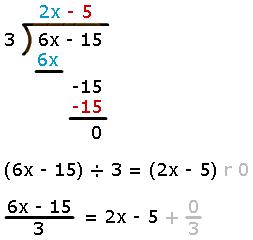
6x - 15 is the dividend.
3 is the divisor.
2x - 5 is the quotient.
0 is the remainder.
Since the remainder is zero, both 3 and 2x - 5 are factors of 6x - 15.
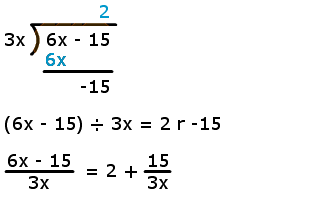
6x - 15 is the dividend.
3x is the divisor.
2 is the quotient.
-15 is the remainder.
Since the remainder is not zero, neither 3x nor 2 are factors of 6x - 15.