Brackets have many specific uses and meanings in mathematics. In algebra they are used to enclose expressions that are intended to be treated as a single term.

Normally an expression is enclosed between an "opening bracket" and a matching "closing bracket" forming a pair of brackets.

When evaluating an expression without brackets, the following are used as the standard order of operations.

The words bracket, parenthesis and brace are generally used interchangeably, even though they represent specific things.

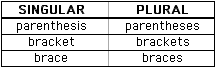
"(" and ")" are properly called "parentheses", "ordinary brackets" or "round brackets".

"[" and "]" are properly called "square brackets".

"{" and "}" are properly called "braces" or "curly brackets".

"<" and ">" are properly called "angle brackets" but are rarely used in the context of "order of operations".

When brackets are nested, sometimes the convention is to use parentheses for all brackets, as in the example expression below left. Sometimes the convention is to use parentheses for the innermost brackets, square brackets for the "next higher level" and braces for the "next higher level", as in the expression below right.

3( 10 - ( 8 - ( 1 + 2 ) ) )                3{ 10 - [ 8 - ( 1 + 2 ) )]}

Each expression represents the same thing..