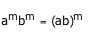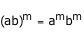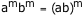If "a" and "b" are non-zero integer and "m" is a whole number, then:

When multiplying powers with a common exponent, the result can be found by multiplying the bases and retaining the exponent.

By the symmetric property of equality, this property can be written either way.

Usually it is written as shown below and is called the "power of a product" property.

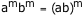
2 x 3 = 6. If the unwritten exponents of one are placed in the equation, it would be written as 2¹3¹ = 6¹.

Notice that the exponents are all the same (one).

2²3² = (4)(9)

2²3² = 36

2²3² = 6²

2⁵3⁵ = (32)(243)

2²3² = 7776

2²3² = 6⁵

Generalization

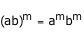
(2x5)³ = (2x5)(2x5)(2x5)          Definition of a power

(2x5)³ = 2x5x2x5x2x5

(2x5)³ = 2x2x2x5x5x5             Rearrange   (Commutative property of multiplication)

(2x5)³ = (2x2x2)(5x5x5)

(2x5)³ = 2³5³

Generalization