Activité
- Pour qu’un polygone soit régulier, il faut que tous ses côtés soient de la même longueur et que ses angles intérieurs soient congruents, donc égaux. Puisque les angles ne sont pas à l’étude en 3e année, la présente leçon propose donc une autre approche.
- Pour déterminer si un polygone est régulier, les élèves devront se baser sur 2 critères, soit :
- tous les côtés doivent avoir la même longueur;
- tous les sommets sont sur un cercle.
- Dans le cas du triangle et du carré, dès que les côtés sont égaux, la figure est automatiquement régulière, mais dans le cas du pentagone par exemple, le fait d’avoir 5 côtés égaux ne suffit pas pour qu’il soit régulier. Voici un exemple :
- Placez les élèves en équipes de 3 ou 4. Remettez à chaque équipe un couvercle de plastique (un couvercle de contenant de margarine ou de crème glacée par exemple). Notez que plus votre couvercle est petit, plus votre cercle sera petit, donc plus l’activité sera difficile pour les élèves lorsqu’ils devront couper 8 côtés par exemple.
- Afin d’éviter le tâtonnement et les erreurs de mesure, veuillez consulter, dans la section Informations pour l’enseignant, les tableaux des longueurs afin de connaitre les mesures des côtés pour chaque polygone selon la grandeur du cercle de votre couvercle.
- Remettez aux élèves les mesures dont ils ont besoin puis laissez-les mesurer, couper et explorer avec les 5 types de polygones.
- Voici des photos démontrant des polygones réguliers dont tous les côtés sont égaux et dont tous les sommets touchent une paroi d’un cercle. Durant leurs explorations, les élèves devraient obtenir des résultats semblables.
- À la suite de cette activité d’exploration, les élèves pourraient maintenant essayer de former des polygones irréguliers, dont tous les côtés ne sont pas égaux, et essayer de les placer à l’intérieur de leur couvercle afin de voir si tous les sommets touchent une paroi du cercle.

 |
||
 |
Informations pour l’enseignant
Tableaux des longueurs :
Pour le triangle :
| Si le couvercle à un rayon* de | et que le polygone a |
la longueur des pailles devrait être de |
5 cm |
3 côtés |
8,7 cm |
6 cm |
3 côtés |
10,4 cm |
7 cm |
3 côtés |
12,1 cm |
8 cm |
3 côtés |
13,9 cm |
9 cm |
3 côtés |
15,6 cm |
10 cm |
3 côtés |
17,3 cm |
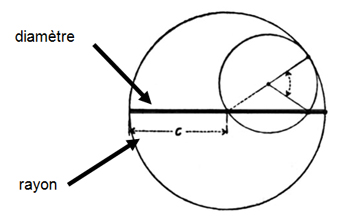
* Le rayon d’un cercle est la moitié de son diamètre :
 |
Pour le carré :
| Si le couvercle à un rayon* de | et que le polygone a |
la longueur des pailles devrait être de |
5 cm |
4 côtés |
7,1 cm |
6 cm |
4 côtés |
8,5 cm |
7 cm |
4 côtés |
9,9 cm |
8 cm |
4 côtés |
11,3 cm |
9 cm |
4 côtés |
12,7 cm |
10 cm |
4 côtés |
14,1 cm |
Pour le pentagone :
| Si le couvercle à un rayon* de | et que le polygone a |
la longueur des pailles devrait être de |
5 cm |
5 côtés |
5,9 cm |
6 cm |
5 côtés |
7,1 cm |
7 cm |
5 côtés |
8,2 cm |
8 cm |
5 côtés |
9,4 cm |
9 cm |
5 côtés |
10,6 cm |
10 cm |
5 côtés |
11,8 cm |
Pour l’hexagone :
| Si le couvercle à un rayon* de | et que le polygone a |
la longueur des pailles devrait être de |
5 cm |
6 côtés |
5 cm |
6 cm |
6 côtés |
6 cm |
7 cm |
6 côtés |
7 cm |
8 cm |
6 côtés |
8 cm |
9 cm |
6 côtés |
9 cm |
10 cm |
6 côtés |
10 cm |
Pour l’octogone :
| Si le couvercle à un rayon* de | et que le polygone a |
la longueur des pailles devrait être de |
5 cm |
8 côtés |
3,8 cm |
6 cm |
8 côtés |
4,6 cm |
7 cm |
8 côtés |
5,4 cm |
8 cm |
8 côtés |
6,1 cm |
9 cm |
8 côtés |
6,9 cm |
10 cm |
8 côtés |
7,7 cm |








