Plan de leçon – Les poignées de main

Police :

Résultat(s) d’apprentissage :

4^e année, Les régularités et les relations, n° 1
5^e année, Les régularités et les relations, n° 1
6^e année, Les régularités et les relations, n° 1

Matériel

Aucun matériel requis

Description :

Les élèves donnent des poignées de main à leurs camarades pour découvrir des régularités entre le nombre de personnes qui se donnent des poignées de main et le nombre de poignées de main.

Activité

L’enseignant soumet le problème suivant à sa classe :
« Dix élèves se présentent à un rassemblement spécialement organisé pour les participants de La grande foire des mathématiques. Et comme ces 10 élèves viennent tous d’écoles différentes, l’enseignant qui a organisé cette rencontre tient vraiment à ce qu’ils fassent connaissance les uns avec les autres. Il demande donc à chacun de se présenter les uns aux autres en se serrant la main. Combien de poignées de mains y aura-t-il eu en tout, une fois cette première étape achevée? »
Trois élèves sont ensuite invités à venir devant la classe. Ces derniers se serrent tous la main une fois, alors que l’enseignant prend en note le nombre de poignées de mains échangées, soit sous la forme d’un dénombrement (tableau, suites numériques, etc.) ou d’une liste organisée de noms.
- Amélie et Félix
- Félix et Carla
- Carla et Amélie

Un autre élève se joint ensuite au groupe précédent, puis chacun des élèves du groupe ainsi formé doit à nouveau jouer son rôle (voir le point 1 ci-dessus) et serrer une fois la main de chacun des 3 autres.

Amélie et Félix
Amélie et Carla
Amélie et Daniel

Félix et Carla
Félix et Daniel

Carla et Daniel

À partir du moment où les groupes atteignent au moins 6 personnes, les élèves doivent déterminer combien de poignées de main sont échangées entre 5 personnes et entre 6 personnes. Les élèves doivent être encouragés à planifier méthodiquement leurs actions. L’enseignant peut, par exemple, leur poser des questions comme la suivante : « Dites-moi, comment pourriez-vous vérifier si vous avez vraiment trouvé toutes les poignées de main possibles? » Pour répondre à cette question, les élèves pourront dresser une liste méthodique, ou alors élaborer des stratégies encore plus complexes. Par exemple :

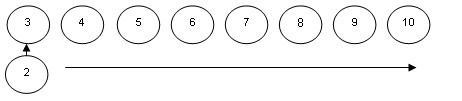
Les élèves du groupe se placent en ligne droite. Le premier élève sort du rang, puis il passe successivement de l’un à l’autre des élèves restants et leur serre la main. Lorsqu’il ne trouve plus personne de nouveau à qui serrer la main, il s’assoit. Ensuite, c’est le deuxième élève qui sort du rang et passe de l’un à l’autre des élèves restants pour leur serrer la main. Cela fait, il s’assoit lui aussi. C’est ensuite le troisième élève du groupe initial qui sort du rang, serre la main à chacun des élèves restants, puis s’assoit… et ainsi de suite. Les élèves poursuivent l’exercice jusqu’à ce qu’il ne reste que 2 élèves du groupe debout. Ces derniers se serrent alors la main, puis ils s’assoient.

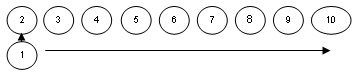
Le premier élève sort du rang, puis il échange une poignée de main avec les 9 autres élèves du groupe.
Les élèves peuvent également former un cercle, serrer la main de leurs voisins, puis serrer la main des autres élèves, tout autour du cercle.

Hexagone montrant toutes les poignées de mains à l'aide de flèches

En comptant les flèches, nous constatons que,
pour un groupe de 6 personnes, 15 échanges
différents de poignées de main sont possibles.

Les élèves consignent leurs résultats dans un tableau. Ils prolongent ensuite la régularité qui en ressort afin de déterminer le nombre maximal de poignées de mains qui pourraient être échangées entre les membres de groupes composés de 2 à 8 personnes.

Nombre de personnes

Nombre de poignées de main

2

1

3

3

4

6

5

10

6

15

7

21

8

28

Deux par deux, les élèves essaient de déterminer combien de poignées de main pourraient être échangées entre 10 élèves et entre 15 élèves. Ils peuvent utiliser une des stratégies suivantes pour visualiser :

Stratégies possibles :

Chaînes d’additions (1^re variante) : Les élèves peuvent utiliser la régularité observée dans une liste méthodique pour créer une chaîne d’additions dont chaque terme est inférieur de 1 au terme précédent.

Amélie-Félix	Félix-Carla	Carla-Daniel	Daniel-Élise	Élise-Mario	Mario-Marc	Marc-Léo	Léo-Lili	Lili-Jean
Amélie-Carla	Félix-Daniel	Carla- Élise	Daniel-Mario	Élise-Marc	Mario-Léo	Marc-Lili	Léo-Jean
Amélie-Daniel	Félix-Élise	Carla- Mario	Daniel-Marc	Élise-Léo	Mario-Lili	Marc-Jean
Amélie-Élise	Félix-Mario	Carla- Marc	Daniel-Léo	Élise-Lili	Mario-Jean
Amélie-Mario	Félix-Marc	Carla- Léo	Daniel-Lili	Élise-Jean
Amélie-Marc	Félix-Léo	Carla- Lili	Daniel-Jean
Amélie-Léo	Félix-Lili	Carla- Jean
Amélie-Lili	Félix-Jean
Amélie-Jean

10 personnes : 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 poignées de main

Chaînes d’additions (2^e variante) : Les élèves peuvent utiliser un diagramme représentant des personnes qui serrent à tour de rôle, et une seule fois, la main de chacune des autres personnes d’un groupe de 10 (ou de 15). Au bout du compte, ils obtiennent la même chaîne d’additions que ci-dessus.

La première personne serre la main des 9 autres personnes, puis elle se retire.

La deuxième personne serre la main des 8 personnes qui restent, puis elle se retire.

La troisième personne serre la main des 7 personnes qui restent, puis elle se retire.
Et ainsi de suite, jusqu’à ce que l’on obtienne ceci :
10 personnes : 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 poignées de main

Diagonales :

Décagone ou tous les sommets sont liés à toutes les diagonales possibles

On peut tracer 9 segments de droites entre chaque (représentation d’une) personne du groupe et les autres, soit 10 x 9 segments de droites dans chaque cas. Toutefois, chacun de ces segments de droites est partagé par 2 personnes. Par conséquent, il y a (10 x 9) ÷ 2 = 45 segments de droites en tout.

Grille : Le nombre possible de poignées de main peut être déterminé à l’aide d’une grille dans laquelle les noms ou les numéros respectifs de chacun des participants identifient, dans le même ordre, chaque rangée et chaque colonne.

Nous comptons donc 10 x 10 = 100 paires, mais nous savons aussi que les personnes ne peuvent pas se serrer la main à elles-mêmes… Par conséquent, nous devons soustraire 10 (paires) de ce nombre, soit :

100 – 10 = 90 …

Mais chacune des paires ainsi dénombrées correspond en réalité à des doublets d’une même action. Par exemple, si 1 serre la main de 2, alors 2 serre du même coup la main de 1… Nous devons donc diviser par 2 le nombre restant de paires (soit 90) pour obtenir, finalement, le nombre possible de poignées de main échangées entre 10 personnes :

90 ÷ 2 = 45 poignées de main.

Informations pour l’enseignant

Il serait important de demander aux élèves de se laver les mains avant le début de cette activité et à la fin. Les poignées de main sont à l’origine de problèmes déjà bien connus partout dans le monde.

Lors de cette activité, les élèves découvrent comment les régularités peuvent être utilisées pour résoudre des problèmes en faisant varier le nombre de personnes qui se serrent la main dans des contextes donnés. Cette tâche d’apprentissage peut être présentée de façon très concrète et les résultats peuvent en être consignés sous la forme d’une liste ordonnée (4^e année); ou alors, elle peut être proposée aux élèves sous une forme purement visuelle, à l’aide d’une variété de diagrammes et de grilles ou de tableaux (5^e et 6^e année).

La relation entre le nombre de personnes (n) et le nombre de poignées de main (p) peut être exprimée ainsi :

formule mathématique

Il doit être clair que nous n’attendons pas des élèves de niveau élémentaire qu’ils arrivent à élaborer de telles formules!

Source : Patterns and Pre-Algebra, Gr. 4-6, Alberta Education, 2007. Activité traduite du cartable publié en anglais.