Lesson 1 - Average Velocity
Average Velocity
explores the difference between average speed and average velocity by moving a ball and
measuring changes in time and position data that is expressed in both Cartesian and Polar notation.
Prerequisites
Students should understand the concepts of displacement and distance traveled.
They will also need a basic understanding of vector quantities.
Learning Outcomes
Students will develop an understanding of average velocity and average speed.
They will also gain more experience in working with vector and scalar quantities.
Instructions
Students should understand the applet functions that are described in Help
and ShowMe. The applet should be open. The step-by-step instructions in this
lesson are to be carried out in the applet. You may need to toggle back and
forth between instructions and applet if your screen space is limited.
Contents
- Notation, Terminology, Definitions
- Average Velocity vs. Average Speed
- A Mistake to Avoid
Before starting the exercises it is important to review some of the key definitions
and notations used in the applet.
Definition 1: Velocity and Speed
Speed
is the rate of change of distance with time, without regard to direction.
Velocity is the rate of change of position with time, and it includes an
expression of direction. |
Expressed in symbols: 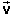 av,
| av,
| 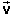 av|, and vav av|, and vav
| Quantity |
Symbol |
SI Unit |
|
Average velocity
(a vector and therefore denoted 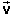 av
in boldface with an arrow on top) av
in boldface with an arrow on top) |
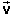 av av |
m/s, direction |
|
Magnitude of the average velocity |
|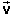 av| av| |
m/s |
|
Average speed
(a scalar and therefore denoted vav in plain
face without an arrow) |
vav |
m/s |
|
| When writing these symbols by hand, the only distinction between them is the arrow. The
arrow indicates velocity, not speed.
The magnitude of the average velocity is in general, not
equal to the average speed. Therefore, a different notation is used
to distinguish between the two. The symbol |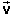 av|
will be used to denote the magnitude (absolute value) of the average
velocity. This is an example where the magnitude of a vector cannot
be denoted by the same symbol as the vector symbol without the arrow. av|
will be used to denote the magnitude (absolute value) of the average
velocity. This is an example where the magnitude of a vector cannot
be denoted by the same symbol as the vector symbol without the arrow.
|
Definition 2: Displacement and
Distance
Distance
traveled is a measure of how far an object has moved. Displacement
is a measure of the magnitude of a change in position and it includes an
expression of direction. |
Expressed in symbols: 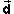 ,
Δ ,
Δ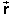 , | , | 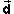 |,
d, and s. |,
d, and s.
| Quantity |
Symbol |
SI Unit |
|
Displacement
(a vector quantity denoted 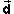 in boldface with
an arrow on top). in boldface with
an arrow on top). |
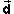 |
m, direction |
|
Another notation for displacement is Δ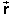 . This notation reflects the fact that displacement is the
difference between two positions (a change in position). . This notation reflects the fact that displacement is the
difference between two positions (a change in position). |
Δ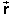 |
m, direction |
|
Magnitude of the Displacement |
|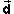 | and d | and d |
m |
|
Distance
(a scalar, denoted s in plain face without an arrow) |
s |
m |
|
| Note that the magnitude (d) of a displacement is in general different from the
distance (s) traveled. |
| Definition 3: Time |
Expressed in symbols: Δt and
t
| Quantity |
Symbol |
SI Unit |
|
Interval of time
The Delta symbol (Δ) indicates a difference or change in time. For
example, the time elapsed between two instants: t1
= 10 s and t2 = 17 s is: Δt
= t2 - t1 = 17 - 10 = 7 s. |
Δt |
s |
|
Instant of time
If one considers a time interval extending from t = 0
to some later instant t of time, the time elapsed is
Δt = t - 0 = t.
In such a case, t can therefore be used to denote time
elapsed. This is what is done in the applet. |
t |
s |
|
Definition 4: Average Velocity and
Average Speed
Average velocity is defined as the ratio: displacement divided by
time elapsed. It has both magnitude and direction. Average speed is defined as the ratio: distance traveled divided by
time elapsed. It does not have an expression of direction. |
Expressed in equations:
| Quantity |
Equation |
SI Unit |
|
Average Velocity
Note that we are dividing a displacement, not a "change"
in a displacement, by the corresponding elapsed time. A displacement
is a change in position; therefore, a "change in displacement"
does not make any sense. |
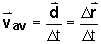 |
m/s, direction |
|
Average Speed |
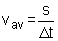 |
m/s |
|
Definition 5: Polar and Cartesian Expressions
The
applet displays the direction for
vector quantities in two forms that will be referred to as Polar and Cartesian. |
| Expression |
Example |
|
Polar
In the Polar form, a vector is specified in terms
of its magnitude and direction relative to the positive x-axis
(in the positive or counter-clockwise direction). |
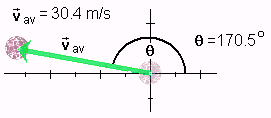
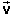 av = (30.4 m/s , 170.5°) av = (30.4 m/s , 170.5°) |
|
Cartesian
In the Cartesian form, a vector is specified in terms
of its x and y components. |
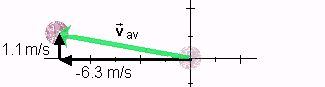
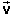 av = (-6.3 , 1.1) m/s av = (-6.3 , 1.1) m/s |
|
Average velocity and average speed are easily illustrated using the applet.

Familiarize
yourself with the applet by completing the following instructions.
- "Reset" (
 )
the applet. )
the applet.
- Turn on the grid lines (
 ). ).
- Position (
 )
the ball at (x, y)i = (10.0, -15.0) m. )
the ball at (x, y)i = (10.0, -15.0) m.
- Drag the ball along any curved path to somewhere near
(x, y)f = (-20.0, -10.0) m.
- Display the initial and final position vectors (
 i
and i
and  f) by clicking
"Position Vector" ( f) by clicking
"Position Vector" ( ). ).
- Display the additional data by clicking "Data" (
 ). ).
With the position vectors and data displayed, you should see something
similar to Figure 1.
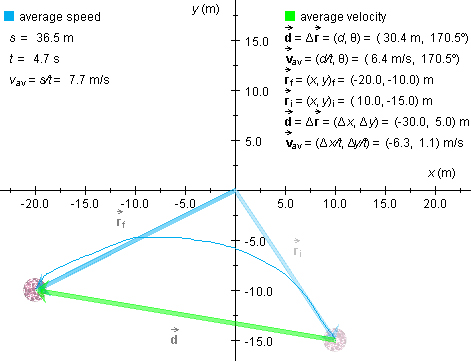
Figure 1
In Figure 1, the following values are included in the display:
- distance traveled: s = 36.5 m
- displacement in the Polar form:
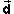 = (d, θ) = (30.4 m, 170.5°)
= (d, θ) = (30.4 m, 170.5°)
- displacement in the Cartesian form:
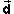 = (Δx, Δy) = (-30.0, 5.0) m
= (Δx, Δy) = (-30.0, 5.0) m
- elapsed time: t = 4.7 s
|
Note that
the time figure given above is based on how quickly the ball was moved from
position 1 to position 2. Your time value should be different than that
which is shown in Figure 1.
Figure 1 also indicates the average speed and average velocity expressed in
both Cartesian and polar form. The following three example problems
illustrate how to calculate average speed and average velocity.
Example Problem 1
Given the distance and
time data, what is the average speed?
|
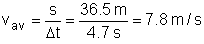 (1) (1)
This agrees with the value displayed in Figure 1. |
Example Problem 2
Given the change in position
and time data, what is the average velocity
expressed in Cartesian notation?
Note that to divide a vector (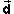 ) by a scalar (Δt),
one divides its x and y components separately by the scalar
(Δt). ) by a scalar (Δt),
one divides its x and y components separately by the scalar
(Δt). |
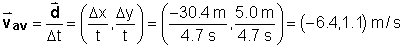 (2) (2)
This agrees with the value displayed in Figure 1. |
Example Problem 3
Given the displacement and time data, what is the average
velocity expressed in Polar notation?
Note that to divide a vector (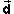 ) by a scalar (t),
one divides its magnitude (d) by the scalar and does not
change the angle. ) by a scalar (t),
one divides its magnitude (d) by the scalar and does not
change the angle. |
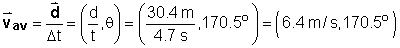 (3) (3)
This agrees with the value displayed in Figure 1. |
Observe that the magnitude of the average velocity has the value |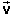 av| = 6.4 m/s and that the average speed has the value vav
= 7.7 m/s. The two values are not equal! This is why the magnitude of
the average velocity cannot be denoted by the symbol vav.
av| = 6.4 m/s and that the average speed has the value vav
= 7.7 m/s. The two values are not equal! This is why the magnitude of
the average velocity cannot be denoted by the symbol vav.

Why is
the average speed greater than the magnitude of the average velocity? Could
there ever be a situation in which it is the other way around? Explain.

Calculate
the average speed and the average velocity (in both the polar and Cartesian
forms) for a ball that is moved according to the following instructions.
- "Reset" (
 )
the applet.
)
the applet.
- Position (
 )
the ball at (x, y)i = (10.0, -5.0) m.
)
the ball at (x, y)i = (10.0, -5.0) m.
- Drag the ball along any curved path to somewhere near (x, y)f
= (-20.0, -10.0) m.
- Display the initial and final position vectors (
 i
and
i
and 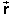 f) by clicking "Position
Vector" (
f) by clicking "Position
Vector" ( ).
).
- Display the additional data by clicking "Data" (
 ).
).
Average Speed calculations:
Average Velocity (Polar) calculations:
|
Average Velocity (Cartesian) calculations:
|

Using the same procedure from Exercise 3, calculate the average speed and the
average velocity (in both the polar and Cartesian forms) for a ball that is
moved from (x, y)i = (0.0, -12.0) m to (x,
y)f = (+5.0, -16.0) m.
Average Speed calculations:
Average Velocity (Polar) calculations:
|
Average Velocity (Cartesian) calculations:
|

Using the same procedure from Exercise 3, calculate the average speed and the
average velocity (in both the polar and Cartesian forms) for a ball that is
moved from (x, y)i = (+6.0, +6.0) m to (x,
y)i = (-4.0, -12.0) m.
Average Speed Calculations:
Average Velocity (Polar) calculations:
|
Average Velocity (Cartesian) calculations:
|
A common mistake is often made when calculating the average speed and
velocity for an object that has changed position several times. The mistake involves
calculating the average speed by combining the speeds of each intermediate motion.
The applet will be used to illustrate how this mistake is made.
Suppose two successive displacements 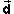 1
and 1
and 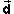 2 are carried out,
as shown in Figure 2. The intermediate point, reached after the first
displacement, is labeled "C". 2 are carried out,
as shown in Figure 2. The intermediate point, reached after the first
displacement, is labeled "C".

Figure 2
Calculating the average speed by combining the speeds of each motion
will require distance and time data for each motion independently. Unfortunately,
the time data related to the intermediate point (C) is not displayed by
the applet after the second displacement has been carried out. In other
words, the time that is displayed in Figure 2 (t = 8.0 s )
is the total time (the time in which both motions occur). To calculate
the speed in each displacement we will need the time elapsed during each
displacement.
|
| How to calculate the average
speed of the first displacement. |
The time value for the first displacement shown in Figure
2 was:
ti-C = 2.5 s
** The elapsed time during the first displacement (from initial position
to position C) was recorded from the applet at the end of the first displacement.
It is not displayed on Figure 2. |
Distance traveled in the first displacement:
|xC - xi| = |xf
- xi| = |-13.5 - 10.0| = 23.5 m |
The average speed during each displacement is calculated
by dividing the distance traveled by the time elapsed. The average speed
of the first displacement:
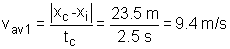 (4) (4)
|
| How to calculate the average speed of the
second displacement. |
The time value for the second displacement shown in Figure
2 must be:
t - tC = 8.0 - 2.5 = 5.5 s
|
Distance traveled in the second displacement:
|yf - yC| = |yf
- yi| = |9.6 - (-12.5)| = 22.1 m |
The average speed of the second displacement:
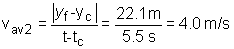 (5) (5)
|
Will combining both individual speeds equal the average speed for the entire
trip?
It may be tempting to work out the answer by taking the average of the two
individual average speeds (4) and (5). This would give the value:
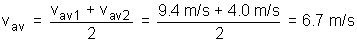 (6)
(6)
However, this value is incorrect because average speed is not
defined as an average of two average speeds over different time intervals. The
correct value shown in Figure 2 is:
vav = 5.7 m/s. (7)
To obtain this value, use 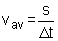 for the average speed.
for the average speed.
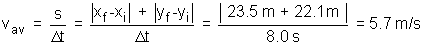 (8)
(8)
Will combining both individual velocities in the Cartesian form equal the average velocity for the entire
trip?
The calculation of each individual velocity is based on Definition (4),
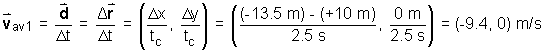 (9)
(9)
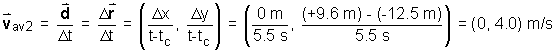 (10)
(10)
Again, the average of these two values is not equal to the average velocity for
the total displacement.
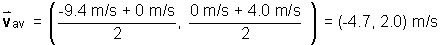 (11)
(11)
The correct value for the average velocity is 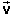 av
= (-2.9, 2.8) m/s, as shown in Figure 2. The correct value is calculated based
on Definition (4). Dividing the total displacement,
av
= (-2.9, 2.8) m/s, as shown in Figure 2. The correct value is calculated based
on Definition (4). Dividing the total displacement, 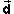 = (-23.5, 22.1) m, by the total time elapsed, Δt
= 8.0 s :
= (-23.5, 22.1) m, by the total time elapsed, Δt
= 8.0 s :
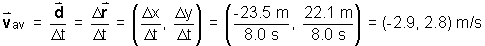 (12)
(12)

A common mistake is often made when calculating the average velocity for an
object that has undergone several different displacements in succession. Describe
this mistake and explain the correct way to determine average velocity in such
cases.
Physics 20-30 v1.0
©2004 Alberta Learning (www.learnalberta.ca)
Last Updated: June 16, 2004
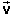 av,
|
av,
| 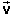 av|, and vav
av|, and vav 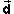 ,
Δ
,
Δ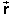 , |
, | 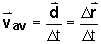
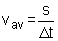




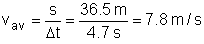 (1)
(1)
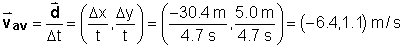 (2)
(2)
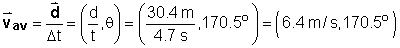 (3)
(3)





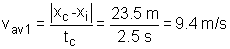 (4)
(4)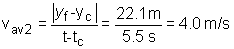 (5)
(5)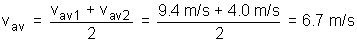 (6)
(6)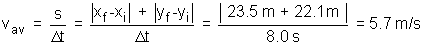 (8)
(8)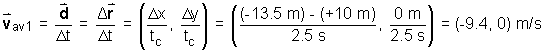 (9)
(9) 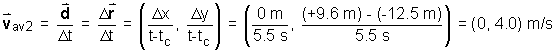 (10)
(10) 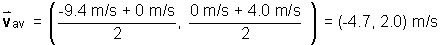 (11)
(11)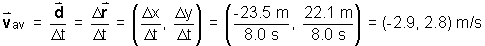 (12)
(12)
