Lesson 1 - Energy Conservation: Weighted Spring
Energy Conservation: Weighted Spring simulates the simple harmonic motion
of a weighted spring in order to graphically explore changes in the weighted
spring's potential and kinetic energy, velocity, and position over time. The
spring constant, mass, and amplitude can be varied.
Prerequisites
Students should be familiar with the general properties of
simple harmonic motion (SHM). Students should also be
familiar with the concepts of kinetic and potential energy
and energy conservation.
Learning Outcomes
Students will learn how to use energy conservation to obtain information
about the potential energy of a weighted spring. They will be able to
describe the time dependence of the potential energy when the spring is
oscillating. They will learn that the energy of the weighted spring is
proportional to the square of the amplitude of oscillation of the spring.
Instructions
Students should understand the applet functions that are described in Help and ShowMe.
The applet should be open. The step-by-step instructions on this page are to
be done in the applet. You may need to toggle back and forth between instructions
and applet if your screen space is limited.
Contents
- Kinetic Energy as a Function of Time
- Potential Energy as a Function of Time
1. Kinetic Energy as a Function of Time
| The kinetic energy KE
of weighted spring varies in time when the weight is oscillating up and
down.

Does the kinetic energy of a weighted spring depend on time t? If
so, how? Use the applet to find out. On the applet,
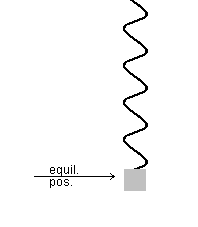
Figure 1
- click "Reset" (
 ) )
- set the spring constant to k = 80 N /m
- keep the mass and the amplitude at their default values of m
= 1.25 kg and A = 0.20 m
- start the motion from its default position, which has the weight in
its top position
- display the position vs. time and velocity vs. time graphs by selecting
them from the graph menu (
 ): ):
|
Sketch the position (y) vs. time (t) and velocity (vy)
vs. time (t) graphs below. On the graphs, mark the points where the spring
passes its top (T), bottom (B), and equilibrium positions (E).
Position vs. Time
Velocity vs. Time


Based on the velocity vs. time graph, is the kinetic energy of the weighted
spring changing with time? Explain.

Sketch the kinetic energy KE of the oscillating spring vs. time by selecting
it from the graph menu ( ) )

Kinetic Energy vs. Time

Does your kinetic energy graph support your answer from Exercise 2? |
| The Kinetic Energy of a spring is related
to its mass (m) amplitude (A), angular frequency (w) and time (t). |
| Expressed as an equation,
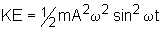 (1)
(1)
| Quantity |
Symbol |
SI Unit |
|
kinetic energy |
KE |
J |
|
mass |
m |
kg |
|
amplitude |
A |
m |
|
angular frequency |
ω |
rad/s |
|
time |
t |
s |
|

Rewind
the applet, and step through the motion until the weight is as close to its
equilibrium point as possible (the energy column would be entirely red at the
equilibrium point). Record the value of the kinetic energy at this point from
the Data box.
KE = _____________ J
Demonstrate how this value is calculated using equation (1).
2. Potential Energy as a Function of Time
The potential energy of the simple pendulum is strictly speaking the
gravitational potential energy of the pendulum-earth system. We will refer
to it as the "potential energy of the pendulum" for short.
The mechanical energy E, energy for short, of
the simple pendulum stays constant during the pendulum's
motion (if the motion is undamped, as it is in the applet).
One says the energy is conserved. The mechanical energy is the
sum of kinetic and potential energy,
E = KE + PE (2)

On the applet, play the motion and observe how there is an ongoing conversion
of potential into kinetic energy or vice versa during the motion even
though the sum of the two energies remains constant. This is observed
by selecting the potential energy, kinetic energy, and mechanical energy
from the graph menu. Sketch all three energy lines on single graph.
Energy vs. Time

|
Now we will use equation (2) together with equation (1)
to obtain information about the time dependence of the
potential energy.

Reset ( )
the applet. )
the applet.
- set the spring constant to k = 80 N /m
- keep the mass and the amplitude at their default values of m
= 1.25 kg and A = 0.20 m
- play the motion
- select the potential energy graph from the graph menu
Sketch a graph of the potential energy as function of time. Mark
the points where the weight passes the top (T), bottom (B), and equilibrium
positions (E).
Potential Energy vs. Time

|
The potential energy at the bob's far right and far left positions and the
value of the mechanical energy are calculated as follows.
The potential energy of the spring is 0 when the weight is at its
equilibrium position. Therefore, at this point, the
mechanical energy E is equal to the kinetic energy
KE (all the energy at the equilibrium position is in the form of
kinetic).
When the weight is either at the top or bottom positions, it is
momentarily at rest and therefore its kinetic energy equals zero. At these
two positions, all the energy is in the form of potential.
Since E is constant during the motion, the potential energy at the
top or bottom is equal to the kinetic energy when the weight is
passing its equilibrium position,
PEtop,bottom = E =
KEmax (3)
Equation (3) combined with equation (1) for the kinetic
energy, is used to derive a general expression for the potential
energy at the top or bottom of the motion and for the
energy E.
|
Potential Energy The potential energy of a weighted spring is
related to its mass (m) amplitude (A), angular frequency (w). |
| Expressed as an equation,
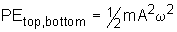 (4)
(4)
| Quantity |
Symbol |
SI Unit |
|
potential energy |
PE |
J |
|
mass |
m |
kg |
|
amplitude |
A |
m |
|
angular frequency |
ω |
rad/s |
|

Use equation (4) to calculate the values of PEtop,bottom
and E for the applet settings in Exercise 6. Verify your answer with
the values in the Data box and also with the value of the kinetic energy near
the equilibrium point determined in Exercise 4 of the previous section. Note:
the latter may not be quite equal to KEmax if you did not
stop the motion at the exact equilibrium point.
There is one other useful equation for determining the potential energy at
the maximum amplitude.
The
angular frequency
w
is related to the spring constant (k) and the mass of the weight (m).
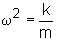 (5)
(5)
Substituting this expression for ω2 into equation (4) gives an
expression for the energy in terms of k and A.
 (6)
(6)

Substitute the applet settings into equation (6) and check if the resulting
value of PEtop,bottom agrees with that obtained in Exercise
7.
Physics 20-30 v1.0
©2004 Alberta Learning (www.learnalberta.ca)
Last Updated: June 16, 2004


 )
) ):
):




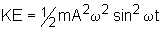 (1)
(1)


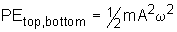 (4)
(4) 
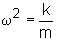 (5)
(5)
 (6)
(6) 
