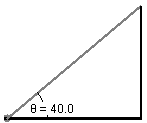Lesson 1 - Inclined Plane, Frictionless
Inclined Plane, Frictionless simulates the motion and forces acting on a
mass moving down a smooth, frictionless incline.
Prerequisites
Students should be
familiar with the concepts of weight and normal force. Students should
also have a working knowledge of free body diagrams and vector component analysis.
Learning Outcomes
Students will be able to construct a free body diagram and determine the net
force acting on an object resting on an incline plane. Students will be able
to calculate the normal force, weight, and weight components acting on an object
on a frictionless incline.
Instructions
Students should understand the applet functions that are described in Help and ShowMe.
The applet should be open. The step-by-step instructions on this page are to
be done in the applet. You may need to toggle back and forth between instructions
and applet if your screen space is limited.
Contents
- Free Body Diagram and Analysis
- The Normal Force
- Questions and Problems
1. Free Body Diagram and Analysis
Free body analysis can be used to determine the observed or net acceleration
of an object that has multiple forces acting on it. For example, consider the
case of a box of crayons resting on a frictionless incline, which is 30°
to the horizontal. The box of crayons will accelerate down the incline at a
rate that is determined by the forces acting on it. The applet will be used
to show these forces.
On the applet, click the "Show FBD" check box ( )
and the "Show FBD Components" check box ( )
to display all of the forces. You can clearly see two forces acting
on the box:
- gravitational force acting straight down
- normal force acting at right angles to the plane of the incline
Sketch and label these two forces on Figure 1 to the right.
Figure 1
|
On the applet, click the "Show FBD" check box ()
and the "Show FBD Components" check box ()
to display all of the forces. Try to reproduce a FBD similar to Figure
2. Define the following vectors:
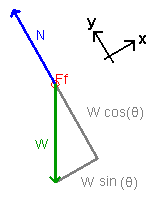
Figure 2
- Normal force (N):
- Weight (W):
Note that Ff indicates the force of
friction is zero
in this example. Also note that the weight force has been resolved into two
components: one component is opposite the normal force while the other
is parallel to the incline. Assume that the "x-direction" is parallel to
the incline and that the "y-direction" is perpendicular to the incline.
 In this
diagram, one of the forces is "balanced" by a component of the
other. Identify these forces.
__________ =
__________
In the configuration shown to the right, will the normal and weight
forces add to give a net force of zero? If not, which force (or component
of force) is not balanced by another force?
________________________
|
Detailed information about the forces is found in the upper right corner
of the drawing panel. From the FBD we conclude that there is:
- a component of the weight that acts perpendicular to the incline,
given by the expression Wy = (W)(cosθ)
- a component of the weight that acts parallel to the incline, given
by the expression Wx = (W)(sinθ)
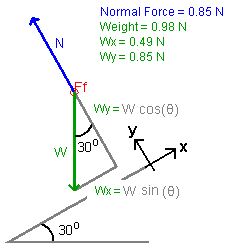
Figure 3
Verify that the magnitude of the components, as given by the applet, are
correct.
Wy =
Wx =
|
2. The Normal Force
| The incline must exert a force on the box of
crayons; otherwise, it would "fall through" the surface. This
force is the normal force, and it is always directed perpendicular to the
surface. Based on Figure 3, the normal force is equal in magnitude to the
component of the object's weight that is perpendicular to the surface of
the incline (Wy). The applet will be used to investigate how the magnitude
of the normal force changes as the angle of the incline is varied. |
|
Set the applet up similar to the Figure 4.
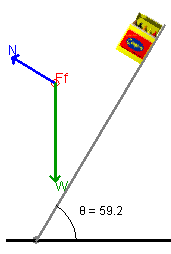
Figure 4
-
As the angle of inclination increases, the magnitude of the normal force
_______________.
-
At any angle of incline the magnitude of the normal force is always
equal to _________________.
|
3. Questions and Problems
On the incline below, draw a free body diagram for a block on an incline
at a 40° angle. Carefully label the incline angle, normal force, weight,
component of weight perpendicular to the surface and the component of
the weight acting parallel to the surface.
|
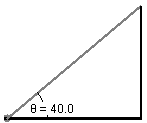
Calculate the magnitude of the normal force from Exercise 7 if the block
has a mass of 1.00 kg. Show your work.
Hint: use the applet to verify your calculations if you "scale"
the applet output by multiplying by the correct scale factor. The applet
uses a 0.100 kg mass; the block mass is 1.00 kg, so the scale
factor is 10.
|
Identify, using your FBD from Exercise 7, which force will cause the 1.00 kg
mass to accelerate if released?
- Calculate the magnitude of this force.
- Calculate the acceleration of the mass using Newton's second law (Fnet = ma).
|
Using the equation from Exercise 9a and Newton's second law (Fnet
= ma), derive an equation that can be used to calculate the acceleration
of any mass on a frictionless incline based only on the acceleration due
to gravity and the incline angle.
|
Use the following information to answer the question below.
| "The Normal Force is always equal to the
weight of the object. It's just the reaction of a surface to an object's weight."
|
If the statement is false, correct it so that it is true. If the statement
is true, explain why it is true.
|
Physics 20-30 v1.0
©2004 Alberta Learning (www.learnalberta.ca)
Last Updated: June 16, 2004