Lesson 1 - 1D Non-Uniform Motion Builder Graphing (pos, vel, acc)

1. The position-time graph for an object is shown below. Reproduce this graph by using 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) and the following settings:
   • Time = 10.0 s
   • Time step = 0.1 s
   • Velocity X = 2.0 m/s
   • Acceleration X = 5.0 m/s²

   

   Plot time on the x-axis and position (x₀) on the y-axis. To help answer these questions, use the fact that slope of a position-time graph is a measure of velocity.

   1. Explain how you can tell, just by visual inspection, that the motion of the object is not uniform, but is speeding up?

2. Use the slope tool () to help complete the following table. From the data you collect, sketch a velocity-time graph in the space provided below. (Tip: double-click on the slope tool button to enter the exact value for the point you wish to examine)

2. Which of the following best describes the velocity-time graph that you made? Write an equation expressing the relation between velocity and time.
   1. the graph is constant and of the mathematical form (b is a constant)
   2. the graph is linear and of the mathematical form (b is a constant and m is the slope)
   3. the graph is a quadratic curve and of the form (where a, b, and c are coefficients)

It is clear from both questions 1 and 2 that the velocity of the object discussed above is not constant. The velocity is continuously changing from a value of 2 m/s to a value of 52 m/s after 10 seconds. You have clear evidence that the object is accelerating.

Now, use 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) to create a velocity-time graph from the same script that you entered in #1. The graph you produce will look very much like the one you made in part 2b. This graph is shown below.

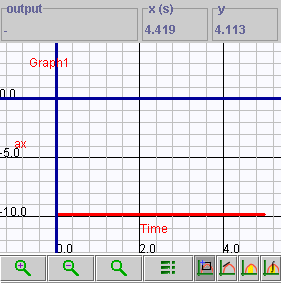
3. What is the slope of this graph? Explain how you determined this.
   
   
   
   
4. What are the units that correctly describe the slope of this graph?
   
   
   
   
   
   
5. What does the slope "mean" here? That is, what quantity of motion does the slope measure?

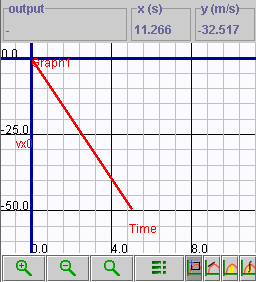
6. The graph shown on the right was produced using 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) and the motion script used in the previous questions. It is an acceleration-time graph. Use 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) to create this graph. In question 3 you determined the slope of the velocity-time graph for the motion. Where or how does that "appear" on this new graph?
   
   
   
   
   
7. What is the slope of the graph shown on the right? What does this "mean" ?

1. In this section, we will explore the idea that area is a measure of the total or cumulative change in some variable. To start this we will use 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) to prepare an acceleration-time graph for a ball falling from rest for 5 seconds. Enter the motion script:
   • Time = 5.0 s
   • Time step = 0.1 s
   • Velocity X = 0.0 m/s
   • Acceleration X = -9.81 m/s²

   

   Next, use the area tool () and measure the area starting from t = 0 s each time. Complete the following table:

2. Each of the areas that you created were simple rectangles. The area of a rectangle is just "length x height".
   1. What units are appropriate for the "length" for each of these rectangles?
   2. What units are appropriate for the "heights" of these rectangles?
   3. What units are appropriate for the areas that you created?

3. The results of question 2 show us that the area of an acceleration-time graph tells us the total change in the velocity of motion. We can do the same thing relating velocity and position. Create a velocity-time graph for the motion script that you used in the previous question. Your graph should look similar to the one shown below.

4. Next, use the area tool () and measure the area starting from t = 0 s each time. Complete the following table:

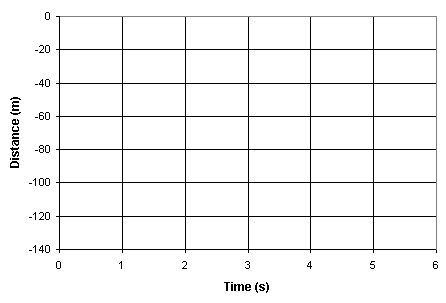
5. Plot the data that you collected in question 3 on the grid provided for you below. Explain what this graph shows. Why are the positions that you are plotting "negative"?

1. You are riding in an elevator. The elevator accelerates upward at 2 m/s² for 5 s and then coasts at a steady speed for 20 s. It then begins to decelerate at 4m/s² for 2.5 s. In the spaces provided below, sketch:
   
   1. the x-t graph for this motion
      
      
      
      
      
   2. the v-t graph for this motion
      
      
      
      
      
   3. the a-t graph for this motion
      
      
      
      
      
   4. What was the maximum speed reached by the elevator?
      
      
      
      
      
   5. How far did the elevator travel while coasting?
      
      
      
      
      
      
   6. How far did the elevator travel while decelerating?

2. Brenda is standing on the edge of a cliff and, as a "physics experiment", tosses her physics book upward with a speed of 22 m/s. It hits the ground at the base of the cliff 6 seconds later. Use 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) to determine how high the cliff is and how fast the book was moving when it landed.
   
   
   
   
   
   
   
   
   
   

3. You are programming a control computer on a subway train. The train accelerates at 2 m/s2. The maximum speed of the subway is 30 m/s. The maximum allowable deceleration rate is 3 m/s2. The total distance that the subway car travels between stops is 1 km. Use 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) to create motion scripts that could accomplish this. Please answer the following:
   
   1. Sketch what the v-t graph should look like for this motion and put your sketch in the place provided below.
      
      .
   2. How much time is spent accelerating?
      
      
      
   3. How far does the subway train travel while accelerating?
      
      
      
   4. How far will the subway travel travel while decelerating?
      
      
      
   5. How much time will it take for the subway train to travel
      between the stops?
      
      
      
   6. What is the average speed of the train as it travels between stops?